Close-up lens

In photography, a close-up lens (sometimes referred to as close-up filter or a macro filter) is a simple secondary lens used to enable macro photography without requiring a specialised primary lens. They work like reading glasses, allowing a primary lens to focus more closely.[1] Bringing the focus closer allows the photographer more possibilities.[2]

Set of three close-up lenses
Typical close-up lens
Optical scheme of close-up photography.
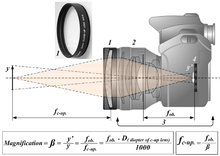
  • 1 - Close-up lens.
  • 2 - Camera objective lens (set to infinity).
  • 3 - Camera.
  • 4 - Film or CCD plane.
  • y - Object
  • y" - Image
Photograph taken with a 3 diopter achromatic close-up lens: Pentatomidae-hatchlings underneath a purple beech leaf

Close-up lenses typically mount on the filter thread of the primary lens,[3] and are often manufactured and sold by suppliers of photographic filters. Nonetheless, they are lenses and not filters. Some manufacturers refer to their close-up lenses as diopters, after the unit of measurement of their optical power.

Close-up lens do not affect exposure, unlike extension tubes, which also can be used for macro photography with a non-macro lens.[4]

Optical power

Close-up lenses are often specified by their optical power in diopters, the reciprocal of the focal length in meters. For a close-up lens, the diopter value is positive: the bigger the number, the greater the effective magnification.

Several close-up lenses may be used in combination; the optical power of the combination is the sum of the optical powers of the component lenses.[5] For example, a set of lenses of +1, +2, and +4 diopters can be combined to provide a range from +1 to +7 in steps of 1.

Working distances and magnifications

Close-up lenses change both the maximum and minimum focus distances of a lens. The range can be rather small.

Working at maximum distance

Adding a close-up lens to a lens focused to infinity changes the focus point to the focal length of the close-up lens, that is, the inverse of its optical power. This is the combination's maximal working distance:

That distance is sometimes given on the filter in mm. A +3 close-up lens has a maximal working distance of 0.333 m or 333 mm.

The magnification is the focal distance of the objective lens (f) divided by the focal distance of the close-up lens; i.e., the focal distance of the objective lens (in meters) multiplied by the diopter value (D) of the close-up lens:

In the example above, if the lens has a 300 mm focal distance, the magnification is 0.3×3 = 0.9.

Given the small size of most sensors (about 25 mm for APS C sensors) a 20 mm insect will almost fill the frame at this magnification. Using a zoom lens makes it easy to frame the subject as desired.

Working at minimal distance

When you add a close-up lens to a camera which is focusing at the shortest distance at which the objective lens can focus, the focus will move to a distance which is given by following formula:

X being the shortest distance at which the objective lens can focus (in meters), and D being the diopter value of the close-up lens. This is the minimal working distance at which you will be able to take a picture with the close-up lens.

For example, a lens that can focus at 1.5 m combined with a +3 diopter close-up lens will give a closest working distance of 1.5/(3×1.5 + 1) = 0.273 m.

The magnification reached in those conditions is given by following formula:

MX being the magnification at distance X without the close-up lens.

In the example above, the gain of magnification at Xmin will be (3×1.5 + 1) = 5.5.

It is at this Xmin distance that you will get the highest magnification.

Macro photography with a close-up lens

Close-up lenses can make a telephoto lens function as a macro lens with a large working distance. This is useful, for example, to prevent scaring small animals or isolating the subject from messy surroundings. To use the filters for animals the size of the animal will determine the working distance (small snakes 1 m to 50 cm, lizards 50–25 cm, small butterflies, beetles 25–10 cm), so it is essential to know what will be the favorite subject before screwing on a close-up lens. The close-up lenses are most effective with long focal length objectives and using a zoom lens is very practical to have some flexibility in the magnification. A good technique for sharp focussing is to take a picture at a long focal length first to have optimal sharpness at the essential details and then zooming out to have the desired size in the frame.

Optical issues

Some single-element close-up lenses produce images with severe aberrations but there are also high-quality close-up lenses composed as achromatic doublets which are capable of producing excellent images, with fairly low loss of sharpness.

gollark: Oh, they will.
gollark: 280 seconds!
gollark: Face reveal, but it's of someone else's face.
gollark: Just 400 seconds left!
gollark: -ioctlo- is actually in the apioform infix table.

See also

References
  1. Meehan, Joseph (2006). The Magic of Digital Close-Up Photography. New York: Lark Books. p. 59. ISBN 978-1-57990-652-8. For real close-up work, some cameras need help—their own version of reading glasses.
  2. Timacheff, Serge (2008). Canon EOS Digital Photography: Photo Workshop. Wiley. p. 8. ISBN 978-0-470-11434-6. ...a variety of accessories increase your creative options. Additional components include Canon Softmat filters and close-up lenses,...
  3. Busch, David D. (2009). Digital SLR Cameras & Photography for Dummies (3rd ed.). Wiley. p. 84. A lot of available add-ons can help you focus close, including filter-like close-up attachments that screw onto the front of the lens,...
  4. Busch, David D. (2009). Digital SLR Cameras & Photography for Dummies (3rd ed.). Wiley. p. 139.
  5. Grimm, Tom; Grimm, Michele (1997). The Basic Book of Photography (4th ed.). Plume. p. 137. ISBN 0-452-27825-2. They can be used alone, or two can be combined.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.