Circular triangle

In geometry, a circular triangle is a triangle with circular arc edges.


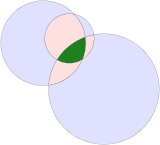Convex circular triangle
Circular horn triangle

Construction
Special cases

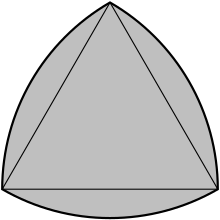Reuleaux triangle
Arbelos

A convex circular triangle may be constructed by three circles intersecting each other and represents the area of intersection. Its edges are all curved outwards. The sum of the internal angles of a circular triangle is greater than 180°. A Reuleaux triangle is a special case based on an equilateral triangle where the center of each arc is on the opposite vertex.

A circular horn triangle is a similar concept, but represents the area interior to 3 mutually tangent circles so all of the internal angles are zero.[1] The arbelos is a special case with three collinear vertices and three semicircular edges.[2]

Other circular triangles can have a mixture of convex and concave circular arc edges.

Long arcs can produce concave figures regardless of whether individual edges are curved inwards or outwards. Inward curved arcs can create self-intersecting forms, such as the a triquetra figure:

Tessellations
Circular tessellation containing lenses and concave circular triangle faces

Circular triangles can be seen in tessellation.

gollark: What? No. Reading's 400WPM or so.
gollark: You just said you typed at 50WPM or so.
gollark: 150WPMish.
gollark: Faster than that, I think?
gollark: Sometimes I plug my phone into my computer and use `scrcpy` to type unreasonably fast on it, for text conversations.

See also

References
  1. The Geometry of the Circular Horn Triangle Edward Kasner and Aida Kalish National Mathematics Magazine Vol. 18, No. 8 (May, 1944), pp. 299–304
  2. Boas, Harold P. (2006), "Reflections on the arbelos" (PDF), American Mathematical Monthly, 113 (3): 236–249, doi:10.2307/27641891, MR 2204487.
  • Richard Courant, Herbert Robbins, What Is Mathematics?: An Elementary Approach to Ideas and Methods, pp. 378–379
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.