Circuit topology

The circuit topology of a linear polymer refers to arrangement of its intra-molecular contacts. Examples of linear polymers with intra-molecular contacts are nucleic acids and proteins. For defining the circuit topology, contacts are defined depending on the context. For proteins with disulfide bonds, these bonds could be considered as contacts. In a context where beta-beta interactions in proteins are more relevant, these interactions are used to define the circuit topology. As such, circuit topology framework can be applied to a wide range of applications including protein folding and analysis of genome architecture.[1] In particular, data from Hi-C and related technologies can be readily analysed using circuit topology framework.

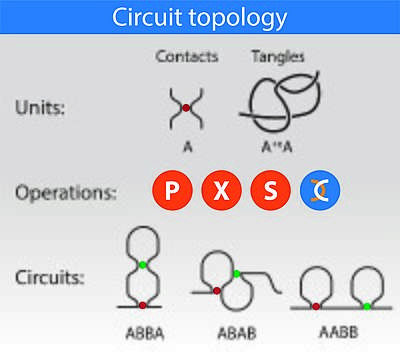
Circuit topology relations in a chain with two binary contacts.
This article is about the topology of polymers. For the topology of electrical circuits, see Topology (electrical circuits).

For a chain with two binary contacts, three arrangements are available: parallel, series and crossed. For a chain with n contacts, the topology can be described by an n by n matrix in which each element illustrates the relation between a pair of contacts and may take one of the three states, P, S and X. Multivalent contacts can also be categorised in full or via decomposition into several binary contacts. Similarly, circuit topology allows for classification of the pairwise arrangements of chain crossings and tangles, thus providing a complete 3D description of folded chains.

Circuit topology has implications for folding kinetics and molecular evolution and has been applied to engineer polymers including protein origami. Circuit topology along with contact order and size are determinants of folding rate of linear polymers.[2] The topology of the cellular proteome and natural RNA reflect evolutionary constraints on biomolecular structures.[3] Topology landscape of biomolecules can be characterized and evolution of molecules can be studied as transition pathways within the landscape.[4]

Further readings
  • B. Scalvini et al. Topology of Folded Molecular Chains: From Single Biomolecules to Engineered Origami. Trends in Chemistry (2020) link
  • M. Heidari et al. Circuit Topology Analysis of Polymer Folding Reactions. ACS Central Science (2020) link
gollark: tar is not a good one.
gollark: You need an archiving format too, except there are no good ones.
gollark: How do you use gzip for version control?
gollark: At GTech™, we just retroactively update all our software instead of versioning it.
gollark: O(x) ∀x

References
  1. Mashaghi, Alireza; van Wijk, Roeland J.; Tans, Sander J. (2014). "Circuit Topology of Proteins and Nucleic Acids". Structure. 22 (9): 1227–1237. doi:10.1016/j.str.2014.06.015. PMID 25126961.
  2. Mugler, Andrew; Tans, Sander J.; Mashaghi, Alireza (2014). "Circuit topology of self-interacting chains: implications for folding and unfolding dynamics". Phys. Chem. Chem. Phys. 16 (41): 22537–22544. Bibcode:2014PCCP...1622537M. doi:10.1039/C4CP03402C.
  3. Mashaghi, Alireza; Ramezanpour, Abolfazl (2015). "Circuit topology of linear polymers: a statistical mechanical treatment". RSC Adv. 5 (64): 51682–51689. arXiv:1509.00432. doi:10.1039/C5RA08106H.
  4. Mashaghi, Alireza; Ramezanpour, Abolfazl (2015). "Distance measures and evolution of polymer chains in their topological space". Soft Matter. 11 (33): 6576–6585. arXiv:1509.00444. Bibcode:2015SMat...11.6576M. doi:10.1039/C5SM01482D.

See also
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.