Chiral polytope

In mathematics, there are two competing definitions for a chiral polytope. One is that it is a polytope that is chiral (or "enantiomorphic"), meaning that it does not have mirror symmetry. By this definition, a polytope that lacks any symmetry at all would be an example of a chiral polytope.

The other, competing definition of a chiral polytope is that it is a polytope that is as symmetric as possible without being mirror-symmetric, formalized in terms of the action of the symmetry group of the polytope on its flags. By this definition, even highly-symmetric and enantiomorphic polytopes such as the snub cube are not chiral. Much of the study of symmetric but chiral polytopes has been carried out in the framework of abstract polytopes, because of the paucity of geometric examples.

Polytopes without mirror symmetry

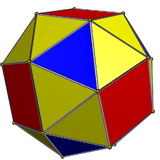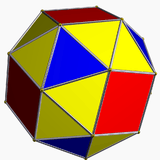
A scalene triangle does not have mirror symmetries, and hence is chiral in 2-dimensions.


The snub cube, vertex-transitive but not mirror-symmetric.

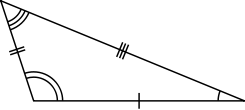
Many polytopes lack mirror symmetry, and in that sense form chiral polytopes. The simplest example is a scalene triangle.[1]

It is possible for polytopes to have a high degree of symmetry, but yet to lack mirror symmetry; an example is the snub cube, which is vertex-transitive and chiral in this sense.[2]

Symmetric chiral polytopes

Definition

The more technical definition of a chiral polytope is a polytope that has two orbits of flags under its group of symmetries, with adjacent flags in different orbits. This implies that it must be vertex-transitive, edge-transitive, and face-transitive, as each vertex, edge, or face must be represented by flags in both orbits; however, it cannot be mirror-symmetric, as every mirror symmetry of the polytope would exchange some pair of adjacent flags.[3]

For the purposes of this definition, the symmetry group of a polytope may be defined in either of two different ways: it can refer to the symmetries of a polytope as a geometric object (in which case the polytope is called geometrically chiral) or it can refer to the symmetries of the polytope as a combinatorial structure (an abstract polytope). Chirality is meaningful for either type of symmetry but the two definitions classify different polytopes as being chiral or nonchiral.[4]

In three dimensions

In three dimensions, it is not possible for a geometrically chiral polytope to have finitely many finite faces. For instance, the snub cube is vertex-transitive, but its flags have more than two orbits, and it is neither edge-transitive nor face-transitive, so it is not symmetric enough to meet the formal definition of chirality. The quasiregular polyhedra and their duals, such as the cuboctahedron and the rhombic dodecahedron, provide another interesting type of near-miss: they have two orbits of flags, but are mirror-symmetric, and not every adjacent pair of flags belongs to different orbits. However, despite the nonexistence of finite chiral three-dimensional polyhedra, there exist infinite three-dimensional chiral skew polyhedra of types {4,6}, {6,4}, and {6,6}.[4]

gollark: Turtle elevator?!

gollark: Dèßpaçîtö.

gollark: That's how I annoyed squid and changed the plethora cost system!

gollark: What steamport said.

gollark: Ish.

References

Tilley, Richard J. D. (2006), Crystals and Crystal Structures, John Wiley & Sons, p. 44, ISBN 9780470018217.
Coxeter, H. S. M. (1995), Kaleidoscopes: Selected Writings, John Wiley and Sons, p. 282, ISBN 9780471010036.
Schulte, Egon; Weiss, Asia Ivić (1991), "Chiral polytopes", in Gritzmann, P.; Sturmfels, B. (eds.), Applied Geometry and Discrete Mathematics (The Victor Klee Festschrift), DIMACS Series in Discrete Mathematics and Theoretical Computer Science, 4, Providence, RI: American Mathematical Society, pp. 493–516, MR 1116373.
Schulte, Egon (2004), "Chiral polyhedra in ordinary space. I" (PDF), Discrete and Computational Geometry, 32 (1): 55–99, doi:10.1007/s00454-004-0843-x, MR 2060817, archived from the original (PDF) on 2010-11-17, retrieved 2012-09-01.