Chebyshev rational functions

In mathematics, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal. They are named after Pafnuty Chebyshev. A rational Chebyshev function of degree n is defined as:

${\displaystyle R_{n}(x)\ {\stackrel {\mathrm {def} }{=}}\ T_{n}\left({\frac {x-1}{x+1}}\right)}$

For the Chebyshev rational functions used in the design of elliptic filters, see Elliptic rational functions.

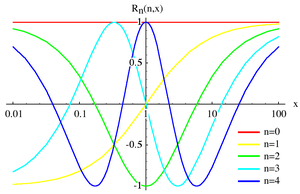
Plot of the Chebyshev rational functions for n = 0, 1, 2, 3, 4 for 0.01 ≤ x ≤ 100, log scale.

where T_n(x) is a Chebyshev polynomial of the first kind.

Properties

Many properties can be derived from the properties of the Chebyshev polynomials of the first kind. Other properties are unique to the functions themselves.

Recursion

${\displaystyle R_{n+1}(x)=2\,{\frac {x-1}{x+1}}R_{n}(x)-R_{n-1}(x)\quad {\text{for }}n\geq 1}$

Differential equations

${\displaystyle (x+1)^{2}R_{n}(x)={\frac {1}{n+1}}{\frac {\mathrm {d} }{\mathrm {d} x}}R_{n+1}(x)-{\frac {1}{n-1}}{\frac {\mathrm {d} }{\mathrm {d} x}}R_{n-1}(x)\quad {\text{for }}n\geq 2}$

${\displaystyle (x+1)^{2}x{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}R_{n}(x)+{\frac {(3x+1)(x+1)}{2}}{\frac {\mathrm {d} }{\mathrm {d} x}}R_{n}(x)+n^{2}R_{n}(x)=0}$

Orthogonality

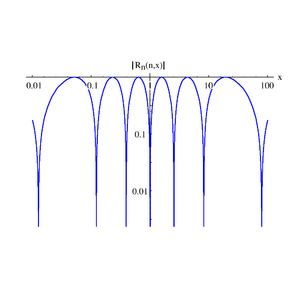
Plot of the absolute value of the seventh-order (n = 7) Chebyshev rational function for 0.01 ≤ x ≤ 100. Note that there are n zeroes arranged symmetrically about x = 1 and if x₀ is a zero, then 1/x₀ is a zero as well. The maximum value between the zeros is unity. These properties hold for all orders.

Defining:

${\displaystyle \omega (x)\ {\stackrel {\mathrm {def} }{=}}\ {\frac {1}{(x+1){\sqrt {x}}}}}$

The orthogonality of the Chebyshev rational functions may be written:

${\displaystyle \int _{0}^{\infty }R_{m}(x)\,R_{n}(x)\,\omega (x)\,\mathrm {d} x={\frac {\pi c_{n}}{2}}\delta _{nm}}$

where c_n = 2 for n = 0 and c_n = 1 for n ≥ 1; δ_nm is the Kronecker delta function.

Expansion of an arbitrary function

For an arbitrary function f(x) ∈ L²
_ω the orthogonality relationship can be used to expand f(x):

${\displaystyle f(x)=\sum _{n=0}^{\infty }F_{n}R_{n}(x)}$

where

${\displaystyle F_{n}={\frac {2}{c_{n}\pi }}\int _{0}^{\infty }f(x)R_{n}(x)\omega (x)\,\mathrm {d} x.}$

Particular values

${\displaystyle {\begin{aligned}R_{0}(x)&=1\\R_{1}(x)&={\frac {x-1}{x+1}}\\R_{2}(x)&={\frac {x^{2}-6x+1}{(x+1)^{2}}}\\R_{3}(x)&={\frac {x^{3}-15x^{2}+15x-1}{(x+1)^{3}}}\\R_{4}(x)&={\frac {x^{4}-28x^{3}+70x^{2}-28x+1}{(x+1)^{4}}}\\R_{n}(x)&=(x+1)^{-n}\sum _{m=0}^{n}(-1)^{m}{\binom {2n}{2m}}x^{n-m}\end{aligned}}}$

Partial fraction expansion

${\displaystyle R_{n}(x)=\sum _{m=0}^{n}{\frac {(m!)^{2}}{(2m)!}}{\binom {n+m-1}{m}}{\binom {n}{m}}{\frac {(-4)^{m}}{(x+1)^{m}}}}$

References

• Guo, Ben-Yu; Shen, Jie; Wang, Zhong-Qing (2002). "Chebyshev rational spectral and pseudospectral methods on a semi-infinite interval" (PDF). Int. J. Numer. Meth. Engng. 53: 65–84. CiteSeerX 10.1.1.121.6069. doi:10.1002/nme.392. Retrieved 2006-07-25.