Channel surface

A channel or canal surface is a surface formed as the envelope of a family of spheres whose centers lie on a space curve, its directrix. If the radii of the generating spheres are constant the canal surface is called pipe surface. Simple examples are:

• right circular cylinder (pipe surface, directrix is a line, the axis of the cylinder)
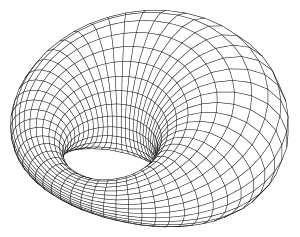
• torus (pipe surface, directrix is a circle),
• right circular cone (canal surface, directrix is a line (the axis), radii of the spheres not constant),
• surface of revolution (canal surface, directrix is a line),

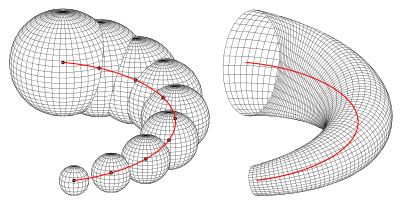
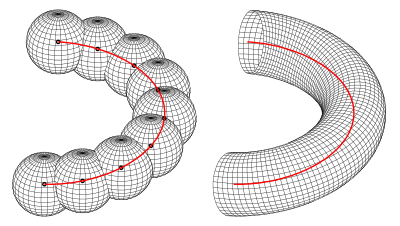
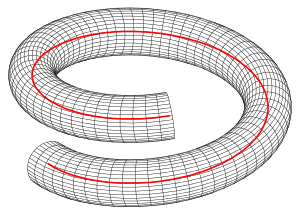
canal surface: directrix is a helix, with its generating spheres

pipe surface: directrix is a helix, with generating spheres

pipe surface: directrix is a helix

Canal surfaces play an essential role in descriptive geometry, because in case of an orthographic projection its contour curve can be drawn as the envelope of circles.

• In technical area canal surfaces can be used for blending surfaces smoothly.

Envelope of a pencil of implicit surfaces

Given the pencil of implicit surfaces

${\displaystyle \Phi _{c}:f({\mathbf {x} },c)=0,c\in [c_{1},c_{2}]}$.

Two neighboring surfaces ${\displaystyle \Phi _{c}}$ and ${\displaystyle \Phi _{c+\Delta c}}$ intersect in a curve that fulfills the equations

${\displaystyle f({\mathbf {x} },c)=0}$ and ${\displaystyle f({\mathbf {x} },c+\Delta c)=0}$.

For the limit ${\displaystyle \Delta c\to 0}$ one gets ${\displaystyle f_{c}({\mathbf {x} },c)=\lim _{\Delta \to \ 0}{\frac {f({\mathbf {x} },c)-f({\mathbf {x} },c+\Delta c)}{\Delta c}}=0}$. The last equation is the reason for the following definition

• Let be ${\displaystyle \Phi _{c}:f({\mathbf {x} },c)=0,c\in [c_{1},c_{2}]}$ a 1-parameter pencil of regular implicit ${\displaystyle C^{2}}$ - surfaces (${\displaystyle f}$ is at least twice continuously differentiable). The surface defined by the two equations

  ${\displaystyle f({\mathbf {x} },c)=0,\quad f_{c}({\mathbf {x} },c)=0}$

is the envelope of the given pencil of surfaces.[1]

Canal surface

Let be ${\displaystyle \Gamma$ :{\mathbf {x} }={\mathbf {c} }(u)=(a(u),b(u),c(u))^{\top }} a regular space curve and ${\displaystyle r(t)}$ a ${\displaystyle C^{1}}$ -function with ${\displaystyle r>0}$ and ${\displaystyle |{\dot {r}}|<\|{\dot {\mathbf {c} }}\|}$. The last condition means that the curvature of the curve is less than that of the corresponding sphere.

The envelope of the 1-parameter pencil of spheres

${\displaystyle f({\mathbf {x} };u):={\big (}{\mathbf {x} }-{\mathbf {c} }(u){\big )}^{2}-r(u)^{2}=0}$

is called canal surface and ${\displaystyle \Gamma }$ its directrix. If the radii are constant, it is called pipe surface.

Parametric representation of a canal surface

The envelope condition

${\displaystyle f_{u}({\mathbf {x} },u):=2{\Big (}{\big (}{\mathbf {x} }-{\mathbf {c} }(u){\big )}{\dot {\mathbf {c} }}(u)-r(u){\dot {r}}(u){\Big )}=0}$,

of the canal surface above is for any value of ${\displaystyle u}$ the equation of a plane, which is orthogonal to the tangent ${\displaystyle {\dot {\mathbf {c} }}(u)}$ of the directrix . Hence the envelope is a collection of circles. This property is the key for a parametric representation of the canal surface. The center of the circle (for parameter ${\displaystyle u}$) has the distance ${\displaystyle d:={\frac {r{\dot {r}}}{\|{\dot {\mathbf {c} }}\|}}<r}$ (s. condition above) from the center of the corresponding sphere and its radius is ${\displaystyle {\sqrt {r^{2}-d^{2}}}}$. Hence

• ${\displaystyle {\mathbf {x} }={\mathbf {x} }(u,v):={\mathbf {c} }(u)-{\frac {r(u){\dot {r}}(u)}{\|{\dot {\mathbf {c} }}(u)\|^{2}}}{\dot {\mathbf {c} }}(u)+{\frac {r(u){\sqrt {\|{\dot {\mathbf {c} }}(u)\|^{2}-{\dot {r}}^{2}}}}{\|{\dot {\mathbf {c} }}(u)\|}}{\big (}{\mathbf {e} }_{1}(u)\cos(v)+{\mathbf {e} }_{2}(u)\sin(v){\big )},}$

where the vectors ${\displaystyle {\mathbf {e} }_{1},{\mathbf {e} }_{2}}$ and the tangenten vector ${\displaystyle {\dot {\mathbf {c} }}}$ form an orthonormal basis, is a parametric representation of the canal surface.[2]

For ${\displaystyle {\dot {r}}=0}$ one gets the parametric representation of a pipe surface:

• ${\displaystyle {\mathbf {x} }={\mathbf {x} }(u,v):={\mathbf {c} }(u)+r{\big (}{\mathbf {e} }_{1}(u)\cos(v)+{\mathbf {e} }_{2}(u)\sin(v){\big )}.}$

pipe knot

canal surface: Dupin cyclide

Examples

a) The first picture shows a canal surface with

1. the helix ${\displaystyle (\cos(u),\sin(u),0.25u),u\in [0,4]}$ as directrix and
2. the radius function ${\displaystyle r(u):=0.2+0.8u/2\pi }$.
3. The choice for ${\displaystyle {\mathbf {e} }_{1},{\mathbf {e} }_{2}}$ is the following:

${\displaystyle {\mathbf {e} }_{1}:=({\dot {b}},-{\dot {a}},0)/\|\cdots \|,\ {\mathbf {e} }_{2}:=({\mathbf {e} }_{1}\times {\dot {\mathbf {c} }})/\|\cdots \|}$.

b) For the second picture the radius is constant:${\displaystyle r(u):=0.2}$, i. e. the canal surface is a pipe surface.

c) For the 3. picture the pipe surface b) has parameter ${\displaystyle u\in [0,7.5]}$.

d) The 4. picture shows a pipe knot. Its directrix is a curve on a torus

e) The 5. picture shows a Dupin cyclide (canal surface).

References

1. Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 115
2. Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 117

• Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. p. 219. ISBN 0-8284-1087-9.

External links

• M. Peternell and H. Pottmann: Computing Rational Parametrizations of Canal Surfaces