Central place theory

Central place theory is a geographical theory that seeks to explain the number, size and location of human settlements in a residential system.[1] It was introduced in 1933 to explain the spatial distribution of cities across the landscape.[2] The theory was first analyzed by German geographer Walter Christaller, who asserted that settlements simply functioned as 'central places' providing services to surrounding areas.[1]

Building the theory

To develop the theory, Christaller made the following simplifying assumptions:[3]

All areas have:

  • an unbounded isotropic (all flat), homogeneous, limitless surface (abstract space)
  • an evenly distributed population
  • all settlements are equidistant and exist in a triangular lattice pattern
  • evenly distributed resources
  • distance decay mechanism
  • perfect competition and all sellers are economic people maximizing their profits
  • consumers are of the same income level and same shopping behaviour
  • all consumers have a similar purchasing power and demand for goods and services.
  • Consumers visit the nearest central places that provide the function which they demand. They minimize the distance to be travelled
  • no provider of goods or services is able to earn excess profit (each supplier has a monopoly over a hinterland)

Therefore, the trade areas of these central places who provide a particular good or service must all be of equal size

  • there is only one type of transport and this would be equally easy in all directions
  • transport cost is directly proportional to distance travelled

The theory then relied on two concepts: threshold and range.

  • Threshold is the minimum market (population or income) needed to bring about the selling of a particular good or service.
  • Range is the maximum distance consumers are prepared to travel to acquire goods - at some point the cost or inconvenience will outweigh the need for the good.

The result of these consumer preferences is that a system of centers of various sizes will emerge. Each center will supply particular types of goods forming levels of hierarchy. In the functional hierarchies, generalizations can be made regarding the spacing, size and function of settlements.

  1. The larger the settlements are in size, the fewer in number they will be, i.e. there are many small villages, but few large cities.
  2. The larger the settlements grow in size, the greater the distance between them, i.e. villages are usually found close together, while cities are spaced much further apart.
  3. As a settlement increases in size, the range and number of its functions will increase .
  4. As a settlement increases in size, the number of higher-order services will also increase, i.e. a greater degree of specialization occurs in the services.

The higher the order of the goods and services (more durable, valuable and variable), the larger the range of the goods and services, the longer the distance people are willing to travel to acquire them.

At the base of the hierarchy pyramid are shopping centres, newsagents etc. which sell low order goods. These centres are small. At the top of the pyramid are centres selling high order goods. These centres are large. Examples for low order goods and services are: newspaper stalls, groceries, bakeries and post offices. Examples for high order goods and services include jewelry, large shopping malls and arcades. They are supported by a much larger threshold population and demand.

Predictions

He deduced that settlements would tend to form in a triangular/hexagonal lattice, as it is the most efficient pattern to serve areas without any overlap.[1]

In the orderly arrangement of an urban hierarchy, seven different principal orders of settlement have been identified by Christaller, providing different groups of goods and services. Settlement are regularly spaced - equidistant spacing between same order centers, with larger centers farther apart than smaller centers. Settlements have hexagonal market areas, and are most efficient in number and functions.

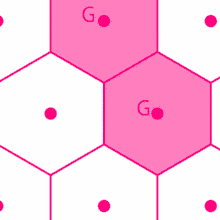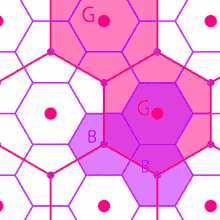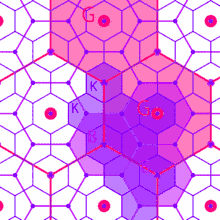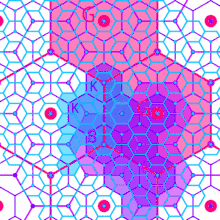
The different layouts predicted by Christaller have K-values which show how much the Sphere of Influence of the central places takes in — the central place itself counts as 1 and each portion of a satellite counts as its portion:

K = 3 marketing principle
K = 3 Principle

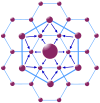
According to the marketing principle K = 3, the market area of a higher-order place (node) occupies one-third of the market area of each of the consecutive lower size place (node) that lies on its neighbour; the lower size nodes (6 in numbers and second larger circles) are located at the corner of a largest hexagon around low value the high-order settlement. Each high-order settlement gets one-third of each satellite settlement (which are 6 in total), thus K = 1 + 6 × ​1⁄3 = 3.

However, in this K = 3 marketing network the distance traveled is minimized.

K = 4 transport/traffic principle
K = 4 Principle

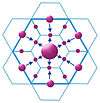
According to K = 4 transport principle, the market area of a higher-order place includes a half of the market area of each of the six neighbouring lower-order places, as they are located on the edges of hexagons around the high-order settlements. This generates a hierarchy of central places which results in the most efficient transport network. There are maximum central places possible located on the main transport routes connecting the higher order center. The transportation principle involves the minimization of the length of roads connecting central places at all hierarchy levels. In this system of nesting, the lower order centres are all located along the roads linking the higher order centres. This alignment of places along a road leads to minimization of road length. However, for each higher order centre, there are now four centres of immediate lower order, as opposed to three centres under the marketing principle.

K = 7 administrative principle
K = 7 Principle

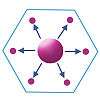
According to K = 7 administrative principle (or political-social principle), settlements are nested according to sevens. The market areas of the smaller settlements are completely enclosed within the market area of the larger settlement. Since tributary areas cannot be split administratively, they must be allocated exclusively to a single higher-order place. Efficient administration is the control principle in this hierarchy.

Evaluation

The validity of the place theory may vary with local factors, such as climate, topography, history of development, technological improvement and personal preference of consumers and suppliers. However, it is still possible to discern Christaller patterns in most distributions of urban centres, even though these patterns will often be distorted by the terrain or imperfect because of suboptimal (with regard to the optimal distribution of centres) historical development decisions.

Economic status of consumers in an area is also important. Consumers of higher economic status tend to be more mobile and therefore bypass centers providing only lower order goods. The application of central place theory must be tempered by an awareness of such factors when planning shopping center space location.

Purchasing power and density affect the spacing of centers and hierarchical arrangements. Sufficient densities will allow, for example, a grocery store, a lower order function, to survive in an isolated location.

Factors shaping the extent of market areas:

  • Land use: industrial areas can provide little in the way of a consuming population
  • Poor accessibility: this can limit the extent of a center's market area
  • Competition: this limits the extent of market areas in all directions
  • Technology: high mobility afforded by the automobile allows overlapping of market areas

Market area studies provide another technique for using central place theory as a retail location planning tool. The hierarchy of shopping centers has been widely used within the planning of "new towns". In this new town, the hierarchy of business centers is evident. One main shopping center provides mostly durable goods (higher order); district and local shopping centers supply, increasingly, convenience (lower order) goods. These centers provided for in the new town plan are not free from outside competition. The impacts of surrounding existing centers on the new town centers cannot be ignored.

Examples

The newly reclaimed polders of the Netherlands provide an isotropic plane on which settlements have developed and in certain areas 6 small towns can be seen surrounding a larger town, especially in the Noord-Oostpolder and Flevoland. The Fens of East Anglia in the UK also provide a large expanse of flat land with no natural barriers to settlement development. Cambridge is a good example of a K=4 Transport Model Central Place, although it is surrounded by 7, rather than 6, settlements. Each satellite is 10–15 miles from Cambridge and each lies on a major road leading out of Cambridge:

As all of the satellite settlements are on transport links, this is a good example of a K=4 CPT model (although in this case it is K=4.5 due to 7 rather than 6 settlements).

Another example of the use of CPT was in the delineation of Medical Care Regions in California. A hierarchy of primary, secondary and tertiary care cities was described, and the population size and income needed to support each medical care specialty in California determined.

Criticism

The central place theory has been criticized for being static; it does not incorporate the temporal aspect in the development of central places. Furthermore, the theory holds up well when it comes to agricultural areas, but not industrial or postindustrial areas due to their diversified nature of various services or their varied distribution of natural resources.

Newer developments: a dynamic concept for CPT

Newer theoretical developments have shown that it is possible to overcome the static aspect of CPT. Veneris (1984) developed a theoretical model which starts with (a) a system of evenly distributed ("medieval") towns; (b) new economic activities are located in some towns thus causing differentiation and evolution into an hierarchical ("industrial") city system; (c) further differentiation leads into a post-hierarchical ("postindustrial") city system.

This evolution can be modelled by means of the three major CPT theories: stage (a) is a system of von Thünen "isolated states"; stage (b) is a Christallerian hierarchical system; stage (c) is a Löschian post-hierarchical system. Furthermore, stage (b) corresponds to Christopher Alexander's "tree" city, while (c) is similar to his "lattice" system (following his dictum "the city is not a tree").

The importance of a city and other theoretical considerations

According to Margot Smith, Walter Christaller erred in his development of CPT in 1930 by using size of population and number of telephones in determining the importance of a city. Smith recognized that although population size was important to the area served by a city, the number of kinds of services offered there was more important as a measure of the importance of a city in attracting consumers. In applying CPT to describe the delivery of medical care in California, Smith counted the number of physician specialties to determine the importance of a city in the delivery of medical care.

Christaller also erred in the assumption that cities "emerge". In California and much of the United States, many cities were situated by the railroads at the time the tracks were laid. In California, towns founded by the railroads were 12 miles apart, the amount of track a section crew could maintain in the 1850s; larger towns were 60 miles apart, the distance a steam engine could travel before needing water. Older towns were founded a day's horse ride apart by the Spanish priests who founded early missions.

In medical care regions described by Smith, there is a hierarchy of services, with primary care ideally distributed throughout an area, middle sized cities offering secondary care, and metropolitan areas with tertiary care. Income, size of population, population demographics, distance to the next service center, all had an influence on the number and kind of specialists located in a population center. (Smith, 1977, 1979)

For example, orthopedic surgeons are found in ski areas, obstetricians in the suburbs, and boutique specialties such as hypnosis, plastic surgery, psychiatry are more likely to be found in high income areas. It was possible to estimate the size of population (threshold) needed to support a specialty, and also to link specialties that needed to cooperate and locate near each other, such as hematology, oncology, and pathology, or cardiology, thoracic surgery and pulmonology.

Her work is important for the study of physician location—where physicians choose to practice and where their practices will have a sufficient population size to support them. The income level of the population determines whether sufficient physicians will practice in an area and whether public subsidy is needed to maintain the health of the population.

The distribution of medical care in California followed patterns having to do with the settlement of cities. Cities and their hinterlands having characteristics of the Traffic Principle (See K=4 above) usually have six thoroughfares through them—the thoroughfares including highways, rivers, railroads, and canals. They are most efficient and can deliver the lowest cost services because transportation is cheaper. Those having settled on the market principle (K=3 above) have more expensive services and goods, as they were founded at times when transportation was more primitive. In Appalachia, for example, the market principle still prevails and rural medical care is much more expensive.

Making central place theory operational

CPT is often criticized as being "unrealistic". However, several studies show that it can describe existing urban systems. An important issue is that Christaller's original formulation is incorrect in several ways (Smith). These errors become apparent if we try to make CPT "operational", that is if we try to derive numerical data out of the theoretical schemata. These problems have been identified for by Veneris (1984) and subsequently by Openshaw and Veneris (2003), who provided also theoretically sound and consistent solutions, based on a K=3, 37-centre CP system:

  1. Closure problem. Christaller's original scheme implies an infinite landscape. Although each market has finite size, the total system has no boundaries to it. Neither Christaller, nor the early related literature provide any guidance as to how the system can be "contained". Openshaw and Veneris (2003) identified three different types of closure, namely (a) isolated state, (b) territorial closure and (c) functional closure. Each closure type implies different population patterns.
  2. Generating trips. Following the basic Christallerian logic and the closure types identified, Openshaw and Veneris (2003) calculate trip patterns between the 27 centres.
  3. Calculating inter- and intra-zonal costs/distances. Christaller assumed freedom of movement in all directions, which would imply "airline" distances between centres. At the same time, he provided specific road networks for the CP system, which do not allow for airline distances. This is a major flaw which neither Christaller, nor early related literature have identified. Openshaw and Veneris (2003) calculate costs/distances which are consistent with the Christallerian principles.

Central place theory and spatial interaction models

It was once thought that central place theory is not compatible with spatial interaction models (SIM). It is paradoxical however that some times towns or shopping centres are planned with CPT, and subsequently evaluated with SIM.

Openshaw and Veneris (2003) succeeded in linking these two major regional theories in a clear and theoretically consistent way: using the data they derived from the operationalization of CPT, they experimented with several SIM. Following a thorough investigation via computer simulation, they reached important theoretical and practical conclusions.

Smith was able to delineate medical care regions (the range), describe the hierarchy of medical services, the population base required of each medical specialty (threshold), the efficiency of regions, and the importance of how an area was settled to the delivery of medical care, that is, according to traffic, market or administrative principles. What is central place?

gollark: They would be roughly as meaningful.
gollark: What if we *randomly generate* horizontal stripe patterns?
gollark: Or is it?
gollark: I don't say 🌵 or <:bees:724389994663247974> for any real clarity.
gollark: > add undefined behavio(u)r flagYes, UB emoji WHEN?

See also

Notes
  1. Goodall, B. (1987) The Penguin Dictionary of Human Geography. London: Penguin.
  2. Caves, R. W. (2004). Encyclopedia of the City. Routledge. p. 73.
  3. http://uprav.ff.cuni.cz/?q=system/files/christaller.pdf

References
  • Openshaw S, Veneris Y, 2003, "Numerical experiments with central place theory and spatial interaction modelling" Environment and Planning A 35(8) 1389–1403 ()
  • Smith, Margot W. Physician's Specialties and Medical Trade Areas: An Application of Central Place Theory. Papers and Proceedings of Applied Geography Conferences, Vol. 9, West Point NY 1986.
  • Smith, Margot W. A Guide to the Delineation of Medical Care Regions, Medical Trade Areas and Hospital Service Areas. Public Health Reports, 94:3:247 May 1979
  • Smith, Margot W. The Economics of Physician Location, Western Regional Conference, American Association of Geographers, Chicago, Illinois, 1979
  • Smith, Margot W. The Distribution of Medical Care in Central California: a Social and Economic Analysis, Thesis, School of Public Health, University of California, Berkeley, 1977 - 1004 pages
  • Veneris, Y, 1984, Informational Revolution, Cybernetics and Urban Modelling, PhD Thesis, University of Newcastle upon Tyne, UK.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.