Center of curvature
In geometry, the center of curvature of a curve is found at a point that is at a distance from the curve equal to the radius of curvature lying on the normal vector. It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the centre of curvature. Cauchy defined the center of curvature C as the intersection point of two infinitely close normal lines to the curve.[1] The locus of centers of curvature for each point on the curve comprise the evolute of the curve. This term is generally used in physics regarding to study of lenses and mirrors.

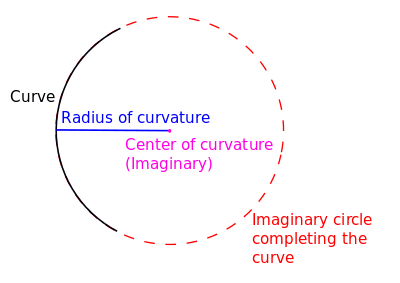
It can also be defined as the spherical distance between the point at which all the rays falling on a lens or mirror either seems to converge to (in the case of convex lenses and concave mirrors) or diverge from (in the case of concave lenses or convex mirrors) and the lens/mirror itself.[2]
See also
- Curvature
- Differential geometry of curves
References
-
- Borovik, Alexandre; Katz, Mikhail G. (2011), "Who gave you the Cauchy--Weierstrass tale? The dual history of rigorous calculus", Foundations of Science, 17 (3): 245–276, arXiv:1108.2885, doi:10.1007/s10699-011-9235-x
- Trinklein, Frederick E. (1992). Modern physics (7th ed.). Austin: Holt, Rinehart and Winston. ISBN 0-03-074317-6. OCLC 25702491.CS1 maint: date and year (link)
Bibliography
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-0087-9