Center manifold

In the mathematics of evolving systems, the concept of a center manifold was originally developed to determine stability of degenerate equilibria. Subsequently, the concept of center manifolds was realised to be fundamental to mathematical modelling.

A bouncing ball. The motion is well described by Newton's laws, except during a bounce when we should consider the ball's deformation.

Consider the example of a ball thrown into the air. Newton's laws of motion assert that we may predict the ball's motion, its evolution, by solving differential equations for its position and velocity. Now what happens when the ball bounces upon impact? A bouncing ball deforms/squashes when it bounces, and Newton can no longer predict the evolution. Instead we may employ the equations of continuum mechanics to describe how all the particles that make up the ball interact during the squashing bounce. After the bounce, the squashing deformation rapidly disappears to leave the ball obeying Newton's laws again. When we view a ball as being made of many interacting component parts, then Newton's description of the ball in terms of just position and velocity (together with spinning modes) is the center manifold of the deformable ball. [1] That is, a center manifold gives the evolution of the relatively simple variables that emerge when a system has many decaying interacting components.

Center manifolds play an important role in: bifurcation theory because interesting behavior takes place on the center manifold; and multiscale mathematics because the long time dynamics of the micro-scale often are attracted to a relatively simple center manifold involving the coarse scale variables.

Definition

Center (red) and unstable (green) manifolds of saddle-node equilibrium point of the system ${\displaystyle {\dot {x}}=x^{2},}$ ${\displaystyle {\dot {y}}=y}$.

Randomly selected points of the 2D phase space converge exponentially to a 1D center manifold on which dynamics are slow (non exponential). Studying dynamics of the center manifold determines the stability of the non-hyperbolic fixed point at the origin.

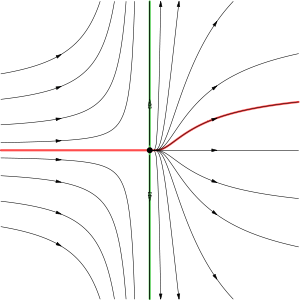
The center manifold of a dynamical system is based upon an equilibrium point of that system—for a ball the equilibrium is the ball at rest and undeformed. A center manifold of the equilibrium then consists of those nearby orbits that neither decay exponentially quickly, nor grow exponentially quickly—for a ball, these include the moving (and spinning) motions in the center manifold, but do not include the ball deforming as such deformations decay exponentially due to damping.

Mathematically, the first step when studying equilibrium points of dynamical systems is to linearize the system, and then compute its eigenvalues and eigenvectors. The eigenvectors (and generalized eigenvectors if they occur) corresponding to eigenvalues with negative real part form a basis for the stable eigenspace. The (generalized) eigenvectors corresponding to eigenvalues with positive real part form the unstable eigenspace. If the equilibrium point is hyperbolic (that is, all eigenvalues of the linearization have nonzero real part), then the Hartman-Grobman theorem guarantees that these eigenvalues and eigenvectors completely characterise the systems dynamics near the equilibrium.

However, if the equilibrium has eigenvalues whose real part is zero, then the corresponding (generalized) eigenvectors form the center eigenspace—for a ball, the center eigenspace is the entire set of unforced rigid body dynamics. [2] Going beyond the linearization, when we account for perturbations by nonlinearity or forcing in the dynamical system, the center eigenspace deforms to the nearby center manifold. [3] If the eigenvalues are precisely zero (as they are for the ball), rather than just real-part being zero, then the corresponding eigenspace more specifically gives rise to a slow manifold. The behavior on the center (slow) manifold is generally not determined by the linearization and thus may be difficult to construct.

Analogously, nonlinearity or forcing in the system perturbs the stable and unstable eigenspaces to a nearby stable manifold and nearby unstable manifold.[4] These three types of manifolds are three cases of an invariant manifold.

Algebraically, let ${\displaystyle {\frac {d{\textbf {x}}}{dt}}={\textbf {f}}({\textbf {x}})}$ be a dynamical system with equilibrium point ${\displaystyle {\textbf {x}}^{*}}$. The linearization of the system near the equilibrium point is

${\displaystyle {\frac {d{\textbf {x}}}{dt}}=A{\textbf {x}},\quad {\text{where }}A={\frac {d{\textbf {f}}}{d{\textbf {x}}}}({\textbf {x}}^{*}).}$

The Jacobian matrix ${\displaystyle A}$ defines three main subspaces:

• the stable subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues ${\displaystyle \lambda }$ with ${\displaystyle \operatorname {Re} \lambda <0}$;
• the unstable subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues ${\displaystyle \lambda }$ with ${\displaystyle \operatorname {Re} \lambda >0}$;
• the center subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues ${\displaystyle \lambda }$ with ${\displaystyle \operatorname {Re} \lambda =0}$.

Depending upon the application, other subspaces of interest include center-stable, center-unstable, sub-center, slow, and fast subspaces. These subspaces are all invariant subspaces of the linearized equation.

Corresponding to the linearized system, the nonlinear system has invariant manifolds, each consisting of sets of orbits of the nonlinear system.[5]

• An invariant manifold tangent to the stable subspace and with the same dimension is the stable manifold.
• The unstable manifold is of the same dimension and tangent to the unstable subspace.
• A center manifold is of the same dimension and tangent to the center subspace. If, as is common, the eigenvalues of the center subspace are all precisely zero, rather than just real part zero, then a center manifold is often called a slow manifold.

Center manifold theorems

The center manifold existence theorem states that if the right-hand side function ${\displaystyle {\textbf {f}}({\textbf {x}})}$ is ${\displaystyle C^{r}}$ (${\displaystyle r}$ times continuously differentiable), then at every equilibrium point there exists a neighborhood of some finite size in which there is at least one of [6]

• a unique ${\displaystyle C^{r}}$ stable manifold,
• a unique ${\displaystyle C^{r}}$ unstable manifold,
• and a (not necessarily unique) ${\displaystyle C^{r-1}}$ center manifold.

In example applications, a nonlinear coordinate transform to a normal form can clearly separate these three manifolds.[7] A web service currently undertakes the necessary computer algebra for a range of finite-dimensional systems.

In the case when the unstable manifold does not exist, center manifolds are often relevant to modelling. The center manifold emergence theorem then says that the neighborhood may be chosen so that all solutions of the system staying in the neighborhood tend exponentially quickly to some solution ${\displaystyle {\textbf {y}}(t)}$ on the center manifold. That is, ${\displaystyle {\textbf {x}}(t)={\textbf {y}}(t)+{\mathcal {O}}(e^{-\beta 't})\quad {\text{as }}t\to \infty \,,}$ for some rate ${\displaystyle \beta '}$. [8] This theorem asserts that for a wide variety of initial conditions the solutions of the full system decay exponentially quickly to a solution on the relatively low dimensional center manifold.

A third theorem, the approximation theorem, asserts that if an approximate expression for such invariant manifolds, say ${\displaystyle {\textbf {x}}={\textbf {X}}({\textbf {s}})}$, satisfies the differential equation for the system to residuals ${\displaystyle {\mathcal {O}}(|{\textbf {s}}|^{p})}$ as ${\displaystyle {\textbf {s}}\to {\textbf {0}}}$, then the invariant manifold is approximated by ${\displaystyle {\textbf {x}}={\textbf {X}}({\textbf {s}})}$ to an error of the same order, namely ${\displaystyle {\mathcal {O}}(|{\textbf {s}}|^{p})}$.

Center manifolds of infinite-D and/or of non-autonomous systems

However, some applications, such as to dispersion in tubes or channels, require an infinite-dimensional center manifold. [9] The most general and powerful theory was developed by Aulbach and Wanner. [10] [11] [12] They addressed non-autonomous dynamical systems ${\displaystyle {\frac {d{\textbf {x}}}{dt}}={\textbf {f}}({\textbf {x}},t)}$ in infinite dimensions, with potentially infinite dimensional stable, unstable and center manifolds. Further, they usefully generalised the definition of the manifolds so that the center manifold is associated with eigenvalues such that ${\displaystyle |\operatorname {Re} \lambda |\leq \alpha }$, the stable manifold with eigenvalues ${\displaystyle \operatorname {Re} \lambda \leq -\beta <-r\alpha }$, and unstable manifold with eigenvalues ${\displaystyle \operatorname {Re} \lambda \geq \beta >r\alpha }$. They proved existence of these manifolds, and the emergence of a center manifold, via nonlinear coordinate transforms.

Potzsche and Rasmussen established a corresponding approximation theorem for such infinite dimensional, non-autonomous systems. [13]

Alternative backwards theory

All the extant theory mentioned above seeks to establish invariant manifold properties of a specific given problem. In particular, one constructs a manifold that approximates an invariant manifold of the given system. An alternative approach is to construct exact invariant manifolds for a system that approximates the given system---called a backwards theory. The aim is to usefully apply theory to a wider range of systems, and to estimate errors and sizes of domain of validity. [14] [15]

This approach is cognate to the well-established backward error analysis in numerical modeling.

Center manifold and the analysis of nonlinear systems

As the stability of the equilibrium correlates with the "stability" of its manifolds, the existence of a center manifold brings up the question about the dynamics on the center manifold. This is analyzed by the center manifold reduction, which, in combination with some system parameter μ, leads to the concepts of bifurcations.

Correspondingly, two web services currently undertake the necessary computer algebra to construct just the center manifold for a wide range of finite-dimensional systems (provided they are in multinomial form).

• One web service constructs slow manifolds for systems which are linearly diagonalised, but which may be non-autonomous or stochastic.[16]
• Another web service constructs center manifolds for systems with general linearisation, but only for autonomous systems.[17]

Examples

The Wikipedia entry on slow manifolds gives more examples.

A simple example

Consider the system

${\displaystyle {\dot {x}}=x^{2},\quad {\dot {y}}=y.}$

The unstable manifold at the origin is the y axis, and the stable manifold is the trivial set {(0, 0)}. Any orbit not on the stable manifold satisfies an equation of the form ${\displaystyle y=Ae^{-1/x}}$ for some real constant A. It follows that for any real A, we can create a center manifold by piecing together the curve ${\displaystyle y=Ae^{-1/x}}$ for x > 0 with the negative x axis (including the origin). Moreover, all center manifolds have this potential non-uniqueness, although often the non-uniqueness only occurs in unphysical complex values of the variables.

Delay differential equations often have Hopf bifurcations

Another example shows how a center manifold models the Hopf bifurcation that occurs for parameter ${\displaystyle a\approx 4}$ in the delay differential equation ${\displaystyle {dx}/{dt}=-ax(t-1)-2x^{2}-x^{3}}$. Strictly, the delay makes this DE infinite-dimensional.

Fortunately, we may approximate such delays by the following trick that keeps the dimensionality finite. Define ${\displaystyle u_{1}(t)=x(t)}$ and approximate the time-delayed variable, ${\displaystyle x(t-1)\approx u_{3}(t)}$, by using the intermediaries ${\displaystyle {du_{2}}/{dt}=2(u_{1}-u_{2})}$ and ${\displaystyle {du_{3}}/{dt}=2(u_{2}-u_{3})}$.

For parameter near critical, ${\displaystyle a=4+\alpha }$, the delay differential equation is then approximated by the system

${\displaystyle {\frac {d{\textbf {u}}}{dt}}=\left[{\begin{array}{ccc}0&0&-4\\2&-2&0\\0&2&-2\end{array}}\right]{\textbf {u}}+\left[{\begin{array}{c}-\alpha u_{3}-2u_{1}^{2}-u_{1}^{3}\\0\\0\end{array}}\right].}$

Copying and pasting the appropriate entries, the web service finds that in terms of a complex amplitude ${\displaystyle s(t)}$ and its complex conjugate ${\displaystyle {\bar {s}}(t)}$, the center manifold

${\displaystyle {\textbf {u}}=\left[{\begin{array}{c}e^{i2t}s+e^{-i2t}{\bar {s}}\\{\frac {1-i}{2}}e^{i2t}s+{\frac {1+i}{2}}e^{-i2t}{\bar {s}}\\-{\frac {i}{2}}e^{i2t}s+{\frac {i}{2}}e^{-i2t}{\bar {s}}\end{array}}\right]+{O}(\alpha +|s|^{2})}$

and the evolution on the center manifold is

${\displaystyle {\frac {ds}{dt}}=\left[{\frac {1+2i}{10}}\alpha s-{\frac {3+16i}{15}}|s|^{2}s\right]+{O}(\alpha ^{2}+|s|^{4})}$

This evolution shows the origin is linearly unstable for ${\displaystyle \alpha >0\ (a>4)}$, but the cubic nonlinearity then stabilises nearby limit cycles as in classic Hopf bifurcation.

Notes

1. Muncaster, R.G. (1983). "Invariant Manifolds In Mechanics II: Zero-dimensional Elastic Bodies With Directors". Arch. Rat. Mech. Anal. 84 (4): 375–392. Bibcode:1983ArRMA..84..375M. doi:10.1007/BF00250588.
2. Roberts, A.J. (1993). "The invariant manifold of beam deformations. Part 1: the simple circular rod". J. Elas. 30: 1–54. doi:10.1007/BF00041769.
3. Carr, Jack (1981). Applications of centre manifold theory. Applied Mathematical Sciences. 35. Springer-Verlag. doi:10.1007/978-1-4612-5929-9. ISBN 978-0-387-90577-8.
4. Kelley, A. (1967). "The stable, center-stable, center, center-unstable and unstable manifolds". J. Differential Equations. 3 (4): 546–570. Bibcode:1967JDE.....3..546K. doi:10.1016/0022-0396(67)90016-2.
5. Guckenheimer & Holmes (1997), Section 3.2
6. Guckenheimer & Holmes (1997), Theorem 3.2.1
7. Murdock, James (2003). Normal forms and unfoldings for local dynamical systems. Springer-Verlag.
8. Iooss, G.; Adelmeyer, M. (1992). Topics in Bifurcation Theory. p. 7.
9. Roberts, A. J. (1988). "The application of centre manifold theory to the evolution of systems which vary slowly in space". J. Austral. Math. Soc. B. 29 (4): 480–500. doi:10.1017/S0334270000005968.
10. Aulbach, B.; Wanner, T. (1996). "Integral manifolds for Caratheodory type differential equations in Banach spaces". In Aulbach, B.; Colonius, F. (eds.). Six Lectures on Dynamical Systems. Singapore: World Scientific. pp. 45–119.
11. Aulbach, B.; Wanner, T. (1999). "Invariant foliations for Caratheodory type differential equations in Banach spaces". In Lakshmikantham, V.; Martynyuk, A. A. (eds.). Advances of Stability Theory at the End of XX Century. Gordon & Breach.
12. Aulbach, B.; Wanner, T. (2000). "The Hartman–Grobman theorem for Caratheodory-type differential equations in Banach spaces". Nonlinear Analysis. 40: 91–104. doi:10.1016/S0362-546X(00)85006-3.
13. Potzsche, C.; Rasmussen, M. (2006). "Taylor approximation of integral manifolds". Journal of Dynamics and Differential Equations. 18 (2): 427–460. Bibcode:2006JDDE...18..427P. doi:10.1007/s10884-006-9011-8.
14. Roberts, A.J. (2019). "Backwards theory supports modelling via invariant manifolds for non-autonomous dynamical systems". arXiv:1804.06998 [math.DS].
15. Hochs, Peter; Roberts, A.J. (2019). "Normal forms and invariant manifolds for nonlinear, non-autonomous PDEs, viewed as ODEs in infinite dimensions". J. Differential Equations. 267 (12): 7263–7312. arXiv:1906.04420. Bibcode:2019JDE...267.7263H. doi:10.1016/j.jde.2019.07.021.
16. A.J. Roberts (2008). "Normal form transforms separate slow and fast modes in stochastic dynamical systems". Physica A. 387 (1): 12–38. arXiv:math/0701623. Bibcode:2008PhyA..387...12R. doi:10.1016/j.physa.2007.08.023.
17. A.J. Roberts (1997). "Low-dimensional modelling of dynamics via computer algebra". Comput. Phys. Commun. 100 (3): 215–230. arXiv:chao-dyn/9604012. Bibcode:1997CoPhC.100..215R. doi:10.1016/S0010-4655(96)00162-2.

References

• Guckenheimer, John; Holmes, Philip (1997), Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Applied Mathematical Sciences, 42, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90819-9, corrected fifth printing.

External links

• Jack Carr (ed.). "Center manifold". Scholarpedia.