Carnot's theorem (perpendiculars)
Carnot's theorem (named after Lazare Carnot) describes a necessary and sufficient condition for a common point of intersection of three lines being perpendicular to the (extended) sides of triangle. The theorem can also be thought of as a generalisation of the Pythagorean theorem
blue area = red area
Theorem
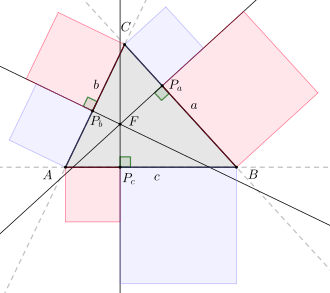
For a triangle with sides consider three lines, which are perpendicular to the triangle sides and intersect in a common point . If are the pedal points of those three perpendiculars on the sides , then the following equation holds:
The converse of the statement above is true as well, that is if the equation holds for the pedal points of three perpendiculars on the three triangle sides then they intersect in a common point. Therefore, the equation provides a necessary and sufficient condition.
Special cases
If the triangle has a right angle in and the intersection point is located on either or , then the equation above yields the Pythagorean theorem. For instance if coincides with then this yields , , , , and . Therefore, the equation above transforms into the Pythagorean theorem .
Another corollary is the property of perpendicular bisectors of a triangle to intersect in a common point. In the case of perpendicular bisectors you have , and and therefore the equation above holds. which means all three perpendicular bisectors intersect in the same point.
References
- Wohlgemuth, Martin., ed. (2010). Mathematisch für fortgeschrittene Anfänger : Weitere beliebte Beiträge von Matroids Matheplanet (in German). Heidelberg: Spektrum Akademischer Verlag. pp. 273–276. ISBN 9783827426079. OCLC 699828882.
- Alfred S. Posamentier; Charles T. Salkind (1996). Challenging problems in geometry. New York: Dover. pp. 85–86. ISBN 9780486134864. OCLC 829151719.
External links
- Florian Modler: Vergessene Sätze am Dreieck - Der Satz von Carnot at matheplanet.com (German)