Céa's lemma

Céa's lemma is a lemma in mathematics. Introduced by Jean Céa in his Ph.D. dissertation, it is an important tool for proving error estimates for the finite element method applied to elliptic partial differential equations.

Lemma statement

Let ${\displaystyle V}$ be a real Hilbert space with the norm ${\displaystyle \|\cdot \|.}$ Let ${\displaystyle a:V\times V\to \mathbb {R} }$ be a bilinear form with the properties

• ${\displaystyle |a(v,w)|\leq \gamma \|v\|\,\|w\|}$ for some constant ${\displaystyle \gamma >0}$ and all ${\displaystyle v,w}$ in ${\displaystyle V}$ (continuity)
• ${\displaystyle a(v,v)\geq \alpha \|v\|^{2}}$ for some constant ${\displaystyle \alpha >0}$ and all ${\displaystyle v}$ in ${\displaystyle V}$ (coercivity or ${\displaystyle V}$-ellipticity).

Let ${\displaystyle L:V\to \mathbb {R} }$ be a bounded linear operator. Consider the problem of finding an element ${\displaystyle u}$ in ${\displaystyle V}$ such that

${\displaystyle a(u,v)=L(v)}$ for all ${\displaystyle v}$ in ${\displaystyle V.}$

Consider the same problem on a finite-dimensional subspace ${\displaystyle V_{h}}$ of ${\displaystyle V,}$ so, ${\displaystyle u_{h}}$ in ${\displaystyle V_{h}}$ satisfies

${\displaystyle a(u_{h},v)=L(v)}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}.}$

By the Lax–Milgram theorem, each of these problems has exactly one solution. Céa's lemma states that

${\displaystyle \|u-u_{h}\|\leq {\frac {\gamma }{\alpha }}\|u-v\|}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}.}$

That is to say, the subspace solution ${\displaystyle u_{h}}$ is "the best" approximation of ${\displaystyle u}$ in ${\displaystyle V_{h},}$ up to the constant ${\displaystyle \gamma /\alpha .}$

The proof is straightforward

${\displaystyle \alpha \|u-u_{h}\|^{2}\leq a(u-u_{h},u-u_{h})=a(u-u_{h},u-v)+a(u-u_{h},v-u_{h})=a(u-u_{h},u-v)\leq \gamma \|u-u_{h}\|\|u-v\|}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}.}$

We used the ${\displaystyle a}$-orthogonality of ${\displaystyle u-u_{h}}$ and ${\displaystyle V_{h}}$

${\displaystyle a(u-u_{h},v)=0,\ \forall \ v\in V_{h}}$

which follows directly from ${\displaystyle V_{h}\subset V}$

${\displaystyle a(u,v)=L(v)=a(u_{h},v)}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}}$.

Note: Céa's lemma holds on complex Hilbert spaces also, one then uses a sesquilinear form ${\displaystyle a(\cdot ,\cdot )}$ instead of a bilinear one. The coercivity assumption then becomes ${\displaystyle |a(v,v)|\geq \alpha \|v\|^{2}}$ for all ${\displaystyle v}$ in ${\displaystyle V}$ (notice the absolute value sign around ${\displaystyle a(v,v)}$).

Error estimate in the energy norm

The subspace solution ${\displaystyle u_{h}}$ is the projection of ${\displaystyle u}$ onto the subspace ${\displaystyle V_{h}}$ in respect to the inner product ${\displaystyle a(\cdot ,\cdot )}$.

In many applications, the bilinear form ${\displaystyle a:V\times V\to \mathbb {R} }$ is symmetric, so

${\displaystyle a(v,w)=a(w,v)}$ for all ${\displaystyle v,w}$ in ${\displaystyle V.}$

This, together with the above properties of this form, implies that ${\displaystyle a(\cdot ,\cdot )}$ is an inner product on ${\displaystyle V.}$ The resulting norm

${\displaystyle \|v\|_{a}={\sqrt {a(v,v)}}}$

is called the energy norm, since it corresponds to a physical energy in many problems. This norm is equivalent to the original norm ${\displaystyle \|\cdot \|.}$

Using the ${\displaystyle a}$-orthogonality of ${\displaystyle u-u_{h}}$ and ${\displaystyle V_{h}}$ and the Cauchy–Schwarz inequality

${\displaystyle \|u-u_{h}\|_{a}^{2}=a(u-u_{h},u-u_{h})=a(u-u_{h},u-v)\leq \|u-u_{h}\|_{a}\cdot \|u-v\|_{a}}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}}$.

Hence, in the energy norm, the inequality in Céa's lemma becomes

${\displaystyle \|u-u_{h}\|_{a}\leq \|u-v\|_{a}}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}}$

(notice that the constant ${\displaystyle \gamma /\alpha }$ on the right-hand side is no longer present).

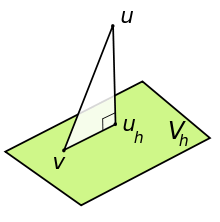
This states that the subspace solution ${\displaystyle u_{h}}$ is the best approximation to the full-space solution ${\displaystyle u}$ in respect to the energy norm. Geometrically, this means that ${\displaystyle u_{h}}$ is the projection of the solution ${\displaystyle u}$ onto the subspace ${\displaystyle V_{h}}$ in respect to the inner product ${\displaystyle a(\cdot ,\cdot )}$ (see the adjacent picture).

Using this result, one can also derive a sharper estimate in the norm ${\displaystyle \|\cdot \|}$. Since

${\displaystyle \alpha \|u-u_{h}\|^{2}\leq a(u-u_{h},u-u_{h})=\|u-u_{h}\|_{a}^{2}\leq \|u-v\|_{a}^{2}\leq \gamma \|u-v\|^{2}}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}}$,

it follows that

${\displaystyle \|u-u_{h}\|\leq {\sqrt {\frac {\gamma }{\alpha }}}\|u-v\|}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}}$.

An application of Céa's lemma

We will apply Céa's lemma to estimate the error of calculating the solution to an elliptic differential equation by the finite element method.

A string with fixed endpoints under the influence of a force pointing down.

Consider the problem of finding a function ${\displaystyle u:[a,b]\to \mathbb {R} }$ satisfying the conditions

${\displaystyle {\begin{cases}-u''=f{\mbox{ in }}[a,b]\\u(a)=u(b)=0\end{cases}}}$

where ${\displaystyle f:[a,b]\to \mathbb {R} }$ is a given continuous function.

Physically, the solution ${\displaystyle u}$ to this two-point boundary value problem represents the shape taken by a string under the influence of a force such that at every point ${\displaystyle x}$ between ${\displaystyle a}$ and ${\displaystyle b}$ the force density is ${\displaystyle f(x)\mathbf {e} }$ (where ${\displaystyle \mathbf {e} }$ is a unit vector pointing vertically, while the endpoints of the string are on a horizontal line, see the adjacent picture). For example, that force may be the gravity, when ${\displaystyle f}$ is a constant function (since the gravitational force is the same at all points).

Let the Hilbert space ${\displaystyle V}$ be the Sobolev space ${\displaystyle H_{0}^{1}(a,b),}$ which is the space of all square-integrable functions ${\displaystyle v}$ defined on ${\displaystyle [a,b]}$ that have a weak derivative on ${\displaystyle [a,b]}$ with ${\displaystyle v'}$ also being square integrable, and ${\displaystyle v}$ satisfies the conditions ${\displaystyle v(a)=v(b)=0.}$ The inner product on this space is

${\displaystyle (v,w)=\int _{a}^{b}\!v'(x)w'(x)\,dx}$ for all ${\displaystyle v}$ and ${\displaystyle w}$ in ${\displaystyle V.}$

After multiplying the original boundary value problem by ${\displaystyle v}$ in this space and performing an integration by parts, one obtains the equivalent problem

${\displaystyle a(u,v)=L(v)}$ for all ${\displaystyle v}$ in ${\displaystyle V,}$

with

${\displaystyle a(u,v)=\int _{a}^{b}\!u'(x)v'(x)\,dx}$

(here the bilinear form is given by the same expression as the inner product, this is not always the case), and

${\displaystyle L(v)=\int _{a}^{b}\!f(x)v(x)\,dx.}$

It can be shown that the bilinear form ${\displaystyle a(\cdot ,\cdot )}$ and the operator ${\displaystyle L}$ satisfy the assumptions of Céa's lemma.

A function in ${\displaystyle V_{h}}$ (in red), and the typical collection of basis functions in ${\displaystyle V_{h}}$ (in blue).

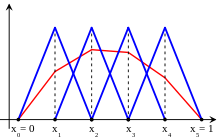
In order to determine a finite-dimensional subspace ${\displaystyle V_{h}}$ of ${\displaystyle V,}$ consider a partition

${\displaystyle a=x_{0}<x_{1}<\cdots <x_{n-1}<x_{n}=b}$

of the interval ${\displaystyle [a,b],}$ and let ${\displaystyle V_{h}}$ be the space of all continuous functions that are affine on each subinterval in the partition (such functions are called piecewise-linear). In addition, assume that any function in ${\displaystyle V_{h}}$ takes the value 0 at the endpoints of ${\displaystyle [a,b].}$ It follows that ${\displaystyle V_{h}}$ is a vector subspace of ${\displaystyle V}$ whose dimension is ${\displaystyle n-1}$ (the number of points in the partition that are not endpoints).

Let ${\displaystyle u_{h}}$ be the solution to the subspace problem

${\displaystyle a(u_{h},v)=L(v)}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h},}$

so one can think of ${\displaystyle u_{h}}$ as of a piecewise-linear approximation to the exact solution ${\displaystyle u.}$ By Céa's lemma, there exists a constant ${\displaystyle C>0}$ dependent only on the bilinear form ${\displaystyle a(\cdot ,\cdot ),}$ such that

${\displaystyle \|u-u_{h}\|\leq C\|u-v\|}$ for all ${\displaystyle v}$ in ${\displaystyle V_{h}.}$

To explicitly calculate the error between ${\displaystyle u}$ and ${\displaystyle u_{h},}$ consider the function ${\displaystyle \pi u}$ in ${\displaystyle V_{h}}$ that has the same values as ${\displaystyle u}$ at the nodes of the partition (so ${\displaystyle \pi u}$ is obtained by linear interpolation on each interval ${\displaystyle [x_{i},x_{i+1}]}$ from the values of ${\displaystyle u}$ at interval's endpoints). It can be shown using Taylor's theorem that there exists a constant ${\displaystyle K}$ that depends only on the endpoints ${\displaystyle a}$ and ${\displaystyle b,}$ such that

${\displaystyle |u'(x)-(\pi u)'(x)|\leq Kh\|u''\|_{L^{2}(a,b)}}$

for all ${\displaystyle x}$ in ${\displaystyle [a,b],}$ where ${\displaystyle h}$ is the largest length of the subintervals ${\displaystyle [x_{i},x_{i+1}]}$ in the partition, and the norm on the right-hand side is the L² norm.

This inequality then yields an estimate for the error

${\displaystyle \|u-\pi u\|.}$

Then, by substituting ${\displaystyle v=\pi u}$ in Céa's lemma it follows that

${\displaystyle \|u-u_{h}\|\leq Ch\|u''\|_{L^{2}(a,b)},}$

where ${\displaystyle C}$ is a different constant from the above (it depends only on the bilinear form, which implicitly depends on the interval ${\displaystyle [a,b]}$).

This result is of a fundamental importance, as it states that the finite element method can be used to approximately calculate the solution of our problem, and that the error in the computed solution decreases proportionately to the partition size ${\displaystyle h.}$ Céa's lemma can be applied along the same lines to derive error estimates for finite element problems in higher dimensions (here the domain of ${\displaystyle u}$ was in one dimension), and while using higher order polynomials for the subspace ${\displaystyle V_{h}.}$

References

• Céa, Jean (1964). Approximation variationnelle des problèmes aux limites (PDF) (PhD thesis). Annales de l'Institut Fourier 14. 2. pp. 345–444. Retrieved 2010-11-27. (Original work from J. Céa)

• Johnson, Claes (1987). Numerical solution of partial differential equations by the finite element method. Cambridge University Press. ISBN 0-521-34514-6.

• Monk, Peter (2003). Finite element methods for Maxwell's equations. Oxford University Press. ISBN 0-19-850888-3.

• Roos, H.-G.; Stynes, M.; Tobiska, L. (1996). Numerical methods for singularly perturbed differential equations: convection-diffusion and flow problems. Berlin; New York: Springer-Verlag. ISBN 3-540-60718-8.

• Eriksson, K.; Estep, D.; Hansbo, P.; Johnson, C. (1996). Computational differential equations. Cambridge; New York: Cambridge University Press. ISBN 0-521-56738-6.

• Zeidler, Eberhard (1995). Applied functional analysis: applications to mathematical physics. New York: Springer-Verlag. ISBN 0-387-94442-7.

• Brenner, Susanne C.; L. Ridgeway Scott (2002). The mathematical theory of finite element methods (2nd ed.). ISBN 0-387-95451-1. OCLC 48892839.
• Ciarlet, Philippe G. (2002). The finite element method for elliptic problems ((SIAM Classics reprint) ed.). ISBN 0-89871-514-8. OCLC 48892573.