Buchstab function

The Buchstab function (or Buchstab's function) is the unique continuous function ${\displaystyle \omega$ :\mathbb {R} _{\geq 1}\rightarrow \mathbb {R} _{>0}} defined by the delay differential equation

${\displaystyle \omega (u)={\frac {1}{u}},\qquad \qquad \qquad 1\leq u\leq 2,}$

${\displaystyle {\frac {d}{du}}(u\omega (u))=\omega (u-1),\qquad u\geq 2.}$

Graph of the Buchstab function ω(u) from u = 1 to u = 4.

In the second equation, the derivative at u = 2 should be taken as u approaches 2 from the right. It is named after Alexander Buchstab, who wrote about it in 1937.

Asymptotics

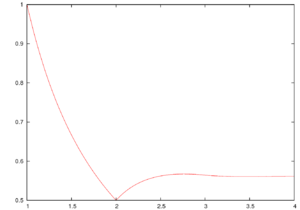
The Buchstab function approaches ${\displaystyle e^{-\gamma }}$ rapidly as ${\displaystyle u\to \infty ,}$ where ${\displaystyle \gamma }$ is the Euler–Mascheroni constant. In fact,

${\displaystyle |\omega (u)-e^{-\gamma }|\leq {\frac {\rho (u-1)}{u}},\qquad u\geq 1,}$

where ρ is the Dickman function.[1] Also, ${\displaystyle \omega (u)-e^{-\gamma }}$ oscillates in a regular way, alternating between extrema and zeroes; the extrema alternate between positive maxima and negative minima. The interval between consecutive extrema approaches 1 as u approaches infinity, as does the interval between consecutive zeroes.[2]

Applications

The Buchstab function is used to count rough numbers. If Φ(x, y) is the number of positive integers less than or equal to x with no prime factor less than y, then for any fixed u > 1,

${\displaystyle \Phi (x,x^{1/u})\sim \omega (u){\frac {x}{\log x^{1/u}}},\qquad x\to \infty .}$

Notes

1. (5.13), Jurkat and Richert 1965. In this paper the argument of ρ has been shifted by 1 from the usual definition.
2. p. 131, Cheer and Goldston 1990.

References

• Бухштаб, А. А. (1937), "Асимптотическая оценка одной общей теоретикочисловой функции" [Asymptotic estimation of a general number-theoretic function], Matematicheskii Sbornik (in Russian), 2(44) (6): 1239–1246, Zbl 0018.24504
• "Buchstab Function", Wolfram MathWorld. Accessed on line Feb. 11, 2015.
• §IV.32, "On Φ(x,y) and Buchstab's function", Handbook of Number Theory I, József Sándor, Dragoslav S. Mitrinović, and Borislav Crstici, Springer, 2006, ISBN 978-1-4020-4215-7.
• "A differential delay equation arising from the sieve of Eratosthenes", A. Y. Cheer and D. A. Goldston, Mathematics of Computation 55 (1990), pp. 129–141.
• "An improvement of Selberg’s sieve method", W. B. Jurkat and H.-E. Richert, Acta Arithmetica 11 (1965), pp. 217–240.
• Hildebrand, A. (2001) [1994], "Bukhstab function", Encyclopedia of Mathematics, EMS Press