Broken diagonal

In recreational mathematics and the theory of magic squares, a broken diagonal is a set of n cells forming two parallel diagonal lines in the square. Alternatively, these two lines can be thought of as wrapping around the boundaries of the square to form a single sequence.

In pandiagonal magic squares

A magic square in which the broken diagonals have the same sum as the rows, columns, and diagonals is called a pandiagonal magic square.[1][2]

Examples of broken diagonals from the number square in the image are as follows: 3,12,14,5; 10,1,7,16; 10,13,7,4; 15,8,2,9; 15,12,2,5; and 6,13,11,4.

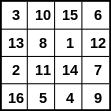
The fact that this square is a pandiagonal magic square can be verified by checking that all of its broken diagonals add up to the same constant:

3+12+14+5=34

10+1+7+16=34

10+13+7+4=34

One way to visualize a broken diagonal is to imagine a "ghost image" of the panmagic square adjacent to the original:

The set of numbers {3, 12, 14, 5} of a broken diagonal, wrapped around the original square, can be seen starting with the first square of the ghost image and moving down to the left.

In linear algebra

Broken diagonals are used in a formula to find the determinant of 3 by 3 matrices.

For a 3 × 3 matrix A, its determinant is

{\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}\Box &\Box &\Box \\\Box &e&f\\\Box &h&i\end{vmatrix}}-b\,{\begin{vmatrix}\Box &\Box &\Box \\d&\Box &f\\g&\Box &i\end{vmatrix}}+c\,{\begin{vmatrix}\Box &\Box &\Box \\d&e&\Box \\g&h&\Box \end{vmatrix}}\\[3pt]&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}

[3]

Here, $bfg,cdh,bdi,$ and $afh$ are broken diagonals of the matrix.

In fact, broken diagonals are used in the calculation of the determinants of all matrices 3 × 3 or larger. This can be shown by using the matrix's minors to calculate the determinant.

gollark: Also manjaro bad.

gollark: The pinephone is not ready for use as a "daily driver".

gollark: That would break the entire notion of derivatives.

gollark: oh apiobees *why*.

gollark: Oops, I accidentally have 9 firefox windows open?>

References

Pickover, Clifford A. (2011), The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across Dimensions, Princeton University Press, p. 7, ISBN 9781400841516.
Licks, H. E. (1921), Recreations in Mathematics, D. Van Nostrand Company, p. 42.
title=Determinant|url=https://mathworld.wolfram.com/Determinant.html

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Pickover, Clifford A. (2011), The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across Dimensions, Princeton University Press, p. 7, ISBN 9781400841516.

[2] Licks, H. E. (1921), Recreations in Mathematics, D. Van Nostrand Company, p. 42.

[3] title=Determinant|url=https://mathworld.wolfram.com/Determinant.html