Brinkmann graph
In the mathematical field of graph theory, the Brinkmann graph is a 4-regular graph with 21 vertices and 42 edges discovered by Gunnar Brinkmann in 1992.[1][2] It was first published by Brinkmann and Meringer in 1997.[3]
| Brinkmann graph | |
|---|---|
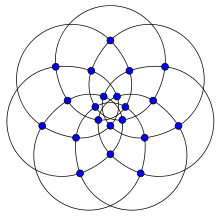 The Brinkmann graph | |
| Named after | Gunnar Brinkmann |
| Vertices | 21 |
| Edges | 42 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 14 (D7) |
| Chromatic number | 4 |
| Chromatic index | 5 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Eulerian Hamiltonian |
| Table of graphs and parameters | |
It has chromatic number 4, chromatic index 5, radius 3, diameter 3 and girth 5. It is also a 3-vertex-connected graph and a 3-edge-connected graph. It is the smallest 4-regular graph of girth 5 with chromatic number 4.[3] It has book thickness 3 and queue number 2.[4]
By Brooks’ theorem, every k-regular graph (except for odd cycles and cliques) has chromatic number at most k. It was also known since 1959 that, for every k and l there exist k-chromatic graphs with girth l.[5] In connection with these two results and several examples including the Chvátal graph, Branko Grünbaum conjectured in 1970 that for every k and l there exist k-chromatic k-regular graphs with girth l.[6] The Chvátal graph solves the case k = l = 4 of this conjecture and the Brinkmann graph solves the case k = 4, l = 5. Grünbaum's conjecture was disproved for sufficiently large k by Johannsen, who showed that the chromatic number of a triangle-free graph is O(Δ/log Δ) where Δ is the maximum vertex degree and the O introduces big O notation.[7] However, despite this disproof, it remains of interest to find examples and only very few are known.
The chromatic polynomial of the Brinkmann graph is x21 - 42x20 + 861x19 - 11480x18 + 111881x17 - 848708x16 + 5207711x15 - 26500254x14 + 113675219x13 - 415278052x12 + 1299042255x11 - 3483798283x10 + 7987607279x9 - 15547364853x8 + 25384350310x7 - 34133692383x6 + 36783818141x5 - 30480167403x4 + 18168142566x3 - 6896700738x2 + 1242405972x (sequence A159192 in the OEIS).
Algebraic properties
The Brinkmann graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 14, the group of symmetries of a heptagon, including both rotations and reflections.
The characteristic polynomial of the Brinkmann graph is .
Gallery
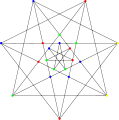 The chromatic number of the Brinkmann graph is 4.
The chromatic number of the Brinkmann graph is 4.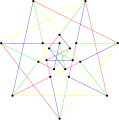 The chromatic index of the Brinkmann graph is 5.
The chromatic index of the Brinkmann graph is 5.
References
- Weisstein, Eric W. "Brinkmann graph". MathWorld.
- Brinkmann, G. "Generating Cubic Graphs Faster Than Isomorphism Checking." Preprint 92-047 SFB 343. Bielefeld, Germany: University of Bielefeld, 1992.
- Brinkmann, G. and Meringer, M. "The Smallest 4-Regular 4-Chromatic Graphs with Girth 5." Graph Theory Notes of New York 32, 40-41, 1997.
- Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- Erdős, Paul (1959), "Graph theory and probability", Canadian Journal of Mathematics, 11 (0): 34–38, doi:10.4153/CJM-1959-003-9.
- Grünbaum, B. (1970), "A problem in graph coloring", American Mathematical Monthly, Mathematical Association of America, 77 (10): 1088–1092, doi:10.2307/2316101, JSTOR 2316101.
- Reed, B. A. (1998), "ω, Δ, and χ", Journal of Graph Theory, 27 (4): 177–212, doi:10.1002/(SICI)1097-0118(199804)27:4<177::AID-JGT1>3.0.CO;2-K.