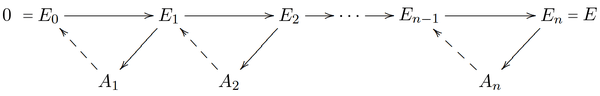Bridgeland stability condition

In mathematics, and especially algebraic geometry, a Bridgeland stability condition, defined by Tom Bridgeland, is an algebro-geometric stability condition defined on elements of a triangulated category. The case of original interest and particular importance is when this derived category is the derived category of coherent sheaves on a Calabi–Yau manifold, and this situation has fundamental links to string theory and the study of D-branes.

Such stability conditions were introduced in a rudimentary form by Michael Douglas called ${\displaystyle \Pi }$-stability and used to study BPS B-branes in string theory.[1] This concept was made precise by Bridgeland, who phrased these stability conditions categorically, and initiated their study mathematically.[2]

Definition

The definitions in this section are presented as in the original paper of Bridgeland, for arbitrary triangulated categories.[2] Let ${\displaystyle {\mathcal {D}}}$ be a triangulated category. A slicing ${\displaystyle {\mathcal {P}}}$ of ${\displaystyle {\mathcal {D}}}$ is a collection of full additive subcategories ${\displaystyle {\mathcal {P}}(\varphi )}$ for each ${\displaystyle \varphi \in \mathbb {R} }$ such that

• ${\displaystyle {\mathcal {P}}(\varphi )[1]={\mathcal {P}}(\varphi +1)}$ for all ${\displaystyle \varphi }$, where ${\displaystyle [1]}$ is the shift functor on the triangulated category,
• if ${\displaystyle \varphi _{1}>\varphi _{2}}$ and ${\displaystyle A\in {\mathcal {P}}(\varphi _{1})}$ and ${\displaystyle B\in {\mathcal {P}}(\varphi _{2})}$, then ${\displaystyle \operatorname {Hom} (A,B)=0}$, and
• for every object ${\displaystyle E\in {\mathcal {D}}}$ there exists a finite sequence of real numbers ${\displaystyle \varphi _{1}>\varphi _{2}>\cdots >\varphi _{n}}$ and a collection of triangles

with ${\displaystyle A_{i}\in {\mathcal {P}}(\varphi _{i})}$ for all ${\displaystyle i}$.

The last property should be viewed as axiomatically imposing the existence of Harder–Narasimhan filtrations on elements of the category ${\displaystyle {\mathcal {D}}}$.

A Bridgeland stability condition on a triangulated category ${\displaystyle {\mathcal {D}}}$ is a pair ${\displaystyle (Z,{\mathcal {P}})}$ consisting of a slicing ${\displaystyle {\mathcal {P}}}$ and a group homomorphism ${\displaystyle Z:K({\mathcal {D}})\to \mathbb {C} }$, where ${\displaystyle K({\mathcal {D}})}$ is the Grothendieck group of ${\displaystyle {\mathcal {D}}}$, called a central charge, satisfying

• if ${\displaystyle 0\neq E\in {\mathcal {P}}(\varphi )}$ then ${\displaystyle Z(E)=m(E)\exp(i\pi \varphi )}$ for some strictly positive real number ${\displaystyle m(E)\in \mathbb {R} _{>0}}$.

It is convention to assume the category ${\displaystyle {\mathcal {D}}}$ is essentially small, so that the collection of all stability conditions on ${\displaystyle {\mathcal {D}}}$ forms a set ${\displaystyle \operatorname {Stab} ({\mathcal {D}})}$. In good circumstances, for example when ${\displaystyle {\mathcal {D}}={\mathcal {D}}^{b}\operatorname {Coh} (X)}$ is the derived category of coherent sheaves on a complex manifold ${\displaystyle X}$, this set actually has the structure of a complex manifold itself.

It is shown by Bridgeland that the data of a Bridgeland stability condition is equivalent to specifying a bounded t-structure ${\displaystyle {\mathcal {P}}(>0)}$ on the category ${\displaystyle {\mathcal {D}}}$ and a central charge ${\displaystyle Z:K({\mathcal {A}})\to \mathbb {C} }$ on the heart ${\displaystyle {\mathcal {A}}={\mathcal {P}}((0,1])}$ of this t-structure which satisfies the Harder–Narasimhan property above.[2] An element ${\displaystyle E\in {\mathcal {A}}}$ is semi-stable (resp. stable) with respect to the stability condition ${\displaystyle (Z,{\mathcal {P}})}$ if for every surjection ${\displaystyle E\to F}$ for ${\displaystyle F\in {\mathcal {A}}}$, we have ${\displaystyle \varphi (E)\leq ({\text{resp.}}<)\,\varphi (F)}$ where ${\displaystyle Z(E)=m(E)\exp(i\pi \varphi (E))}$ and similarly for ${\displaystyle F}$.

References

1. Douglas, M.R., Fiol, B. and Römelsberger, C., 2005. Stability and BPS branes. Journal of High Energy Physics, 2005(09), p. 006.
2. Bridgeland, T., 2007. Stability conditions on triangulated categories. Annals of Mathematics, pp. 317–345.