Bickley–Naylor functions

In physics, engineering, and applied mathematics, the Bickley–Naylor functions are a sequence of special functions arising in formulas for thermal radiation intensities in hot enclosures. The solutions are often quite complicated unless the problem is essentially one-dimensional[1] (such as the radiation field in a thin layer of gas between two parallel rectangular plates). These functions have practical applications in several engineering problems related to transport of thermal[2][3] or neutron[4] radiation in systems with special symmetries (e.g. spherical or axial symmetry). W. G. Bickley was a British mathematician born in 1893.[5]

Definition

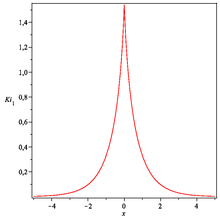
The nth Bickley−Naylor function Ki_n(x) is defined by

${\displaystyle \operatorname {Ki} _{n}(x)=\int _{0}^{\pi /2}e^{-x/\sin \theta }\sin ^{n-1}\theta \,d\theta .}$

and it is classified as one of the generalized exponential integral functions.

Properties

The integral defining the function Ki_n generally cannot be evaluated analytically, but can be approximated to a desired accuracy with Riemann sums or other methods, taking the limit as a → 0 in the interval of integration, [a, π/2].

Alternative ways to define the function Ki_n include the integral[6]

${\displaystyle \operatorname {Ki} _{n}(x)=\int _{0}^{\infty }e^{-x\cosh t}(\cosh t)^{-n}\,dt.}$

All of the functions Ki_n for positive integer n are monotonously decreasing functions, because e^−x is a decreasing function and ${\displaystyle \sin x}$ is a positive increasing function for ${\displaystyle x\in (0,\pi /2)}$.

The values of these functions for different values of the argument x were often listed in tables of special functions in the era when numerical calculation of integrals was slow. A table that lists some approximate values of the three first functions Ki_n is shown below.

x	Ki1(x)	Ki2(x)	Ki3(x)
0	1.57	1.00	0.79
0.2	1.02	0.75	0.61
0.4	0.75	0.58	0.48
0.6	0.56	0.45	0.38
0.8	0.43	0.35	0.30
1.0	0.33	0.27	0.24
1.2	0.25	0.22	0.19
1.4	0.20	0.17	0.15
1.6	0.16	0.14	0.12
1.8	0.12	0.11	0.10

See also

• Exponential integral

References

1. Michael F. Modest, Radiative Heat Transfer, p. 282, Elsevier Science 2003
2. Zekerya Altaḉ, Exact series expansions, recurrence relations, properties and integrals of the generalized exponential integral functions, Journal of Quantitative Spectroscopy & Radiative Transfer 104 (2007) 310–325
3. Z. Altaç, Integrals Involving Bickley and Bessel Functions in Radiative Transfer, and Generalized Exponential Integral Functions, J. Heat Transfer 118(3), 789−792 (August 1, 1996)
4. T. Boševski, An Improved Collision Probability Method for Thermal-Neutron-Flux Calculation in a Cylindrical Reactor Cell, NUCLEAR SCIENCE AND ENGINEERING:. 42, 23−27 (1970)
5. G. S. Marliss W. A. Murray, William G. Bickley—An appreciation, Comput J (1969) 12 (4): 301–302.
6. A. Baricz, T. K. Pogany, Functional Inequalities for the Bickley Function, Mathematical Inequalities and Applications, Volume 17, Number 3 (2014), 989–1003