Balaban 11-cage
In the mathematical field of graph theory, the Balaban 11-cage or Balaban (3-11)-cage is a 3-regular graph with 112 vertices and 168 edges named after Alexandru T. Balaban.[1]
| Balaban 11-cage | |
|---|---|
 The Balaban 11-cage | |
| Named after | Alexandru T. Balaban |
| Vertices | 112 |
| Edges | 168 |
| Radius | 6 |
| Diameter | 8 |
| Girth | 11 |
| Automorphisms | 64 |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Cage Hamiltonian |
| Table of graphs and parameters | |
The Balaban 11-cage is the unique (3-11)-cage. It was discovered by Balaban in 1973.[2] The uniqueness was proved by Brendan McKay and Wendy Myrvold in 2003.[3]
The Balaban 11-cage is a Hamiltonian graph and can be constructed by excision from the Tutte 12-cage by removing a small subtree and suppressing the resulting vertices of degree two.[4]
It has independence number 52,[5] chromatic number 3, chromatic index 3, radius 6, diameter 8 and girth 11. It is also a 3-vertex-connected graph and a 3-edge-connected graph.
Algebraic properties
The characteristic polynomial of the Balaban 11-cage is : .
The automorphism group of the Balaban 11-cage is of order 64.[4]
Gallery
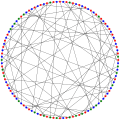 The chromatic number of the Balaban 11-cage is 3.
The chromatic number of the Balaban 11-cage is 3.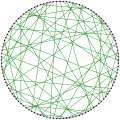 The chromatic index of the Balaban 11-cage is 3.
The chromatic index of the Balaban 11-cage is 3.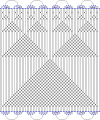 Alternative drawing of the Balaban 11-cage.[6]
Alternative drawing of the Balaban 11-cage.[6]
References
- Weisstein, Eric W. "Balaban 11-Cage". MathWorld.
- Balaban, Alexandru T., Trivalent graphs of girth nine and eleven, and relationships among cages, Revue Roumaine de Mathématiques Pures et Appliquées 18 (1973), 1033-1043. MR0327574
- Weisstein, Eric W. "Cage Graph". MathWorld.
- Geoffrey Exoo & Robert Jajcay, Dynamic cage survey, Electr. J. Combin. 15 (2008)
- Maher Heal (2016)
- P. Eades, J. Marks, P. Mutzel, S. North. "Graph-Drawing Contest Report", TR98-16, December 1998, Mitsubishi Electric Research Laboratories.
References
- Heal, Maher (2016), "A Quadratic Programming Formulation to Find the Maximum Independent Set of Any Graph", The 2016 International Conference on Computational Science and Computational Intelligence, Las Vegas: IEEE Computer Society