Antiprism graph

In the mathematical field of graph theory, an antiprism graph is a graph that has one of the antiprisms as its skeleton. An n-sided antiprism has 2n vertices and 4n edges. They are regular, polyhedral (and therefore by necessity also 3-vertex-connected, vertex-transitive, and planar graphs), and also Hamiltonian graphs.[1]

Examples

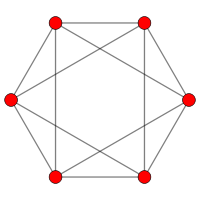
The first graph in the sequence, the octahedral graph, has 6 vertices and 12 edges. Later graphs in the sequence may be named after the type of antiprism they correspond to:


3
4
5
6
7
8

Although geometrically the star polygons also form the faces of a different sequence of (self-intersecting) antiprisms, the star antiprisms, they do not form a different sequence of graphs.

An antiprism graph is a special case of a circulant graph, Ci2n(2,1).

Other infinite sequences of polyhedral graph formed in a similar way from polyhedra with regular-polygon bases include the prism graphs (graphs of prisms) and wheel graphs (graphs of pyramids). Other vertex-transitive polyhedral graphs include the Archimedean graphs.

gollark: With low level stuff being slow and annoying.
gollark: I agree.
gollark: Well, we have several octillion emulated human consciousnesses/bee neurons writing code for us, so probably about 99.99999999%.
gollark: There are things to write bits of your program given a type signature.
gollark: You can implement N-queens in it!

References
  1. Read, R. C. and Wilson, R. J. An Atlas of Graphs, Oxford, England: Oxford University Press, 2004 reprint, Chapter 6 special graphs pp. 261, 270.
  • Weisstein, Eric W. "Antiprism graph". MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.