Andrica's conjecture

Andrica's conjecture (named after Dorin Andrica) is a conjecture regarding the gaps between prime numbers.[1]

(a) The function ${\displaystyle A_{n}}$ for the first 100 primes.

(b) The function ${\displaystyle A_{n}}$ for the first 200 primes.

(c) The function ${\displaystyle A_{n}}$ for the first 500 primes.

Graphical proof for Andrica's conjecture for the first (a)100, (b)200 and (c)500 prime numbers. The function ${\displaystyle A_{n}}$ is always less than 1.

The conjecture states that the inequality

${\displaystyle {\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}<1}$

holds for all ${\displaystyle n}$, where ${\displaystyle p_{n}}$ is the nth prime number. If ${\displaystyle g_{n}=p_{n+1}-p_{n}}$ denotes the nth prime gap, then Andrica's conjecture can also be rewritten as

${\displaystyle g_{n}<2{\sqrt {p_{n}}}+1.}$

Empirical evidence

Imran Ghory has used data on the largest prime gaps to confirm the conjecture for ${\displaystyle n}$ up to 1.3002 × 10¹⁶.[2] Using a table of maximal gaps and the above gap inequality, the confirmation value can be extended exhaustively to 4 × 10¹⁸.

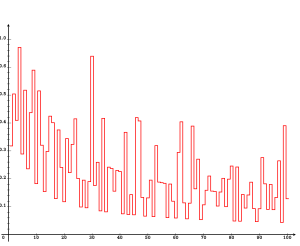
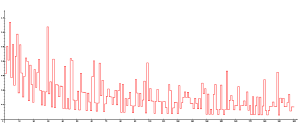
The discrete function ${\displaystyle A_{n}={\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}}$ is plotted in the figures opposite. The high-water marks for ${\displaystyle A_{n}}$ occur for n = 1, 2, and 4, with A₄ ≈ 0.670873..., with no larger value among the first 10⁵ primes. Since the Andrica function decreases asymptotically as n increases, a prime gap of ever increasing size is needed to make the difference large as n becomes large. It therefore seems highly likely the conjecture is true, although this has not yet been proven.

Generalizations

As a generalization of Andrica's conjecture, the following equation has been considered:

${\displaystyle p_{n+1}^{x}-p_{n}^{x}=1,}$

where ${\displaystyle p_{n}}$ is the nth prime and x can be any positive number.

The largest possible solution x is easily seen to occur for ${\displaystyle n=1}$, when x_max = 1. The smallest solution x is conjectured to be x_min ≈ 0.567148... (sequence A038458 in the OEIS) which occurs for n = 30.

This conjecture has also been stated as an inequality, the generalized Andrica conjecture:

${\displaystyle p_{n+1}^{x}-p_{n}^{x}<1}$ for ${\displaystyle x<x_{\min }.}$

See also

• Cramér's conjecture
• Legendre's conjecture
• Firoozbakht's conjecture

References and notes

1. Andrica, D. (1986). "Note on a conjecture in prime number theory". Studia Univ. Babes–Bolyai Math. 31 (4): 44–48. ISSN 0252-1938. Zbl 0623.10030.
2. Prime Numbers: The Most Mysterious Figures in Math, John Wiley & Sons, Inc., 2005, p. 13.

• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. ISBN 978-0-387-20860-2. Zbl 1058.11001.

External links

• Andrica's Conjecture at PlanetMath
• Generalized Andrica conjecture at PlanetMath
• Weisstein, Eric W. "Andrica's Conjecture". MathWorld.