Analemmatic sundial

Analemmatic sundials are a type of horizontal sundial that has a vertical gnomon and hour markers positioned in an elliptical pattern. The gnomon is not fixed and must change position daily to accurately indicate time of day. Hence there are no hour lines on the dial and the time of day is read only on the ellipse.[1] As with most sundials, analemmatic sundials mark solar time rather than clock time. An analemmatic sundial is completely defined by[2][3]

  1. The size of its ellipse (chosen by the designer).
  2. The latitude of its location (determines the location of the hour markers on the ellipse).
  3. The declination of the sun (determines the daily gnomon position).
Analemmatic sundial on a meridian line in the garden of the Herkenrode Abbey in Hasselt (Flanders in Belgium)
Analemmatic sundial at Saint-Etienne, France in which the user's head forms the gnomon of the dial

Analemmatic sundials are sometimes designed with a human as the gnomon. In this case the size of the hour marker ellipse is constrained by human height and the latitude of the sundial location, since the human gnomon shadow must fall on the hour marker ellipse to accurately indicate the time of day. Human gnomon analemmatic sundials are not practical at lower latitudes where a human shadow is quite short during the summer months. A 66-inch tall person casts a 4-inch shadow at 27 deg latitude on the summer solstice.[1]

The use of the adjective "analemmatic" to describe this class of sundial can be misleading, because there is no use of the equation of time or the analemma in the design of an analemmatic sundial. Mayall refers to the analemmatic sundial as "the so-called Analemmatic Dial", implying a lack of connection to the analemma.[4] The dial of Brou in front of the church of Brou in Bourg-en-Bresse, France is an example of the erroneous use of the analemma in the construction of an analemmatic sundial. Rohr states "The gnomon is displaced on the short axis of the ellipse and not on the meridian, whose presence here in the shape of an 8 is a mistake."[5]

Construction
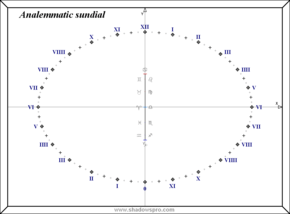
Horizontal analemmatic sundial for 44°29' N drawn with Shadows Expert software. It shows local time
The terminology of sundial classification can be misleading. Although it features an analemma, this analemmic heliochronometer, end of 19th century, is not an analemmatic sundial - refer to the definition given in the text. Exhibit of the National Polytechnic Museum, Sofia

An analemmatic sundial uses a vertical gnomon and its hour lines are the vertical projection of the hour lines of a circular equatorial sundial onto a flat plane.[6] Therefore, the analemmatic sundial is an ellipse, where the short axis is aligned North-South and the long axis is aligned East-West. The noon hour line points true North, whereas the hour lines for 6am and 6pm point due West and East, respectively; the ratio of the short to long axes equals the sine sin(Φ) of the local geographical latitude, denoted Φ. All the hour lines converge to a single centre; the angle θ of a given hour line with the noon hour is given by the formula

where t is the time (in hours) before or after noon.[7]

However, the vertical gnomon does not always stand at the centre of the hour lines; rather, to show the correct time, the gnomon must be moved daily northwards from the centre by the distance

where W is half the width of the ellipse and δ is the Sun's declination at that time of year.[8] The declination measures how far the sun is above the celestial equator; at the equinoxes, δ=0 whereas it equals roughly ±23.5° at the summer and winter solstices.

Declination of the sun
monthJanFebMarAprMayJunJulAugSepOctNovDec
declination -23.13-17.3-84.25152223.00188.50-2.9-14-21.7
Mean values on the first of the month. This averages out the effect of leap years. [9]
gollark: It's compiled. Although there's documentation at the bottom so never mind.
gollark: Hmmmm. I have no idea how to run this.
gollark: Prove it.
gollark: Also, what?
gollark: Which Microsoft?

See also

References
  1. "Analemmatic sundials: How to build one and why they work", C.J. Budd and C.J. Sangwin, maths.org, 1 June 2000
  2. Waugh, (1973) pp. 108-115
  3. Rohr 1970, p. 106
  4. Mayall 1994, p. 186
  5. Rohr 1970, p. 101
  6. Rohr (1965), pp. 100–106; Waugh (1973), pp. 108–115; Mayall and Mayall, p. 60–61, 186–190.
  7. Rohr (1965), p. 106; Waugh (1973), p. 113.
  8. Rohr (1965), pp. 103, 111; Waugh (1973), p. 111.
  9. Pruss, Alexander (2011). "Sun Dial and Paper Craft Generator / Code / [7ac605] /sundial.pl". sourceforge.net. Retrieved 19 May 2018.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.