Algebraic connectivity

The algebraic connectivity (also known as Fiedler value or Fiedler eigenvalue) of a graph G is the second-smallest eigenvalue (counting multiple eigenvalues separately) of the Laplacian matrix of G.[1] This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of connected components in the graph. The magnitude of this value reflects how well connected the overall graph is. It has been used in analysing the robustness and synchronizability of networks.

An example graph, with 6 vertices, diameter 3, connectivity 1, and algebraic connectivity 0.722

Properties
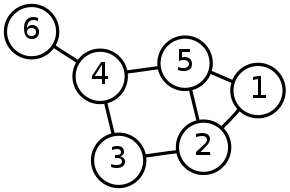
The truncated icosahedron or Buckminsterfullerene graph has a traditional connectivity of 3, and an algebraic connectivity of 0.243.

The algebraic connectivity of a graph G is greater than 0 if and only if G is a connected graph. Furthermore, the value of the algebraic connectivity is bounded above by the traditional (vertex) connectivity of the graph.[2] If the number of vertices of a connected graph is n and the diameter is D, the algebraic connectivity is known to be bounded below by ,[3] and in fact (in a result due to Brendan McKay) by .[4] For the example shown above, 4/18 = 0.222 ≤ 0.722 ≤ 1.

Unlike the traditional connectivity, the algebraic connectivity is dependent on the number of vertices, as well as the way in which vertices are connected. In random graphs, the algebraic connectivity decreases with the number of vertices, and increases with the average degree.[5]

The exact definition of the algebraic connectivity depends on the type of Laplacian used. Fan Chung has developed an extensive theory using a rescaled version of the Laplacian, eliminating the dependence on the number of vertices, so that the bounds are somewhat different.[6]

In models of synchronization on networks, such as the Kuramoto model, the Laplacian matrix arises naturally, so the algebraic connectivity gives an indication of how easily the network will synchronize.[7] Other measures, such as the average distance (characteristic path length) can also be used,[8] and in fact the algebraic connectivity is closely related to the (reciprocal of the) average distance.[4]

The algebraic connectivity also relates to other connectivity attributes, such as the isoperimetric number, which is bounded below by half the algebraic connectivity.[9]

Fiedler vector

The original theory related to algebraic connectivity was produced by Miroslav Fiedler.[10][11] In his honor the eigenvector associated with the algebraic connectivity has been named the Fiedler vector. The Fiedler vector can be used to partition a graph.

Partitioning a graph using the Fiedler vector

For the example graph in the introductory section, the Fiedler vector is . The negative values are associated with the poorly connected vertex 6, and the neighbouring articulation point, vertex 4; while the positive values are associated with the other vertices. The signs of the values in the Fiedler vector can therefore be used to partition this graph into two components: . Alternatively, the value of 0.069 (which is close to zero) can be placed in a class of its own, partitioning the graph into three components: .

gollark: It's not simple because of no generics. It's more complex since they added bodges to work around not having them like the three standard library generic types.
gollark: The code you call simple is long and verbose. The waitgroup thing is a hack because go's got no generics for some sort of parallel map function.
gollark: Haskell is higher level. That means there's less noise to get in the way, unlike Go. Or at least would be, but insane Haskellers add more lots.
gollark: Green threads aren't exactly a new idea. Rust has libraries for that.
gollark: Anyway, they should just have added generics. They improve readability by allowing abstraction.

See also

References
  1. Weisstein, Eric W. "Algebraic Connectivity." From MathWorld--A Wolfram Web Resource.
  2. J.L. Gross and J. Yellen. Handbook of Graph Theory, CRC Press, 2004, page 314.
  3. J.L. Gross and J. Yellen. Handbook of Graph Theory, CRC Press, 2004, page 571.
  4. Bojan Mohar, The Laplacian Spectrum of Graphs, in Graph Theory, Combinatorics, and Applications, Vol. 2, Ed. Y. Alavi, G. Chartrand, O. R. Oellermann, A. J. Schwenk, Wiley, 1991, pp. 871–898.
  5. Synchronization and Connectivity of Discrete Complex Systems, Michael Holroyd, International Conference on Complex Systems, 2006.
  6. F. Chung. Spectral Graph Theory, Providence, RI: Amer. Math. Soc., 1997.
  7. Tiago Pereira, Stability of Synchronized Motion in Complex Networks, arXiv:1112.2297v1, 2011.
  8. D. Watts, Six Degrees: The Science of a Connected Age, Vintage, 2003.
  9. Norman Biggs. Algebraic Graph Theory, 2nd ed, Cambridge University Press, 1993, pp. 28 & 58.
  10. M. Fiedler. "Algebraic connectivity of Graphs", Czechoslovak Mathematical Journal 23(98) (1973), 298–305.
  11. M. Fiedler. "Laplacian of graphs and algebraic connectivity", Combinatorics and Graph Theory (Warsaw, 1987), Banach Center Publications 25(1) (1989), 57–70.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.