Advance ratio

In aeronautics and marine hydrodynamics, the advance ratio is the ratio of the freestream fluid speed to the propeller, rotor, or cyclorotor tip speed. When a propeller-driven vehicle is moving at high speed relative to the fluid, or the propeller is rotating slowly, the advance ratio of its propeller(s) is a high number; and when it is moving at low speed, or the propeller is rotating at high speed, the advance ratio is a low number. The advance ratio is a useful non-dimensional velocity in helicopter and propeller theory, since propellers and rotors will experience the same angle of attack on every blade airfoil section at the same advance ratio regardless of actual forward speed. It is the inverse of the tip speed ratio used for wind turbines.

Diameter of the propeller.

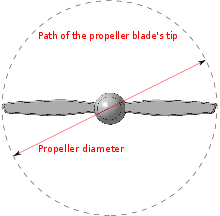
Mathematical definition

Propellers

The advance ratio J is a non-dimensional term given by:[1][2]

${\displaystyle J={\frac {V_{a}}{nD}},}$

where

Va	is the freestream fluid velocity, typically the true airspeed of the aircraft or the water speed of the vessel
n	is the rotations per second of the propeller
D	is the propeller's diameter

Helicopter rotors and cyclorotors

The advance ratio μ is defined as:[3][4]

${\displaystyle \mu ={\frac {V_{\infty }}{\Omega r}},}$

where

V∞	is the freestream fluid velocity, typically the true airspeed of the aircraft or the water speed of the vessel
Ω	is the rotor rotational speed in ${\displaystyle {\frac {rad}{s}}}$
r	is the rotor radius

Significance

Helicopters

Single rotor helicopters are limited in forward speed by a combination of sonic tip speed and retreating blade stall. As the advance ratio increases, the relative velocity experienced by the retreating blade decreases so that the tip of the blade experiences zero velocity at an advance ratio of one. Helicopter rotors pitch the retreating blade to a higher angle of attack to maintain lift as the relative velocity decreases. At a sufficiently high advance ratio, the blade will reach the stalling angle of attack and experience retreating blade stall. Specially designed airfoils can increase the operating advance ratio by utilizing high lift coefficient airfoils. Currently, single rotor helicopters are practically limited to advance ratios less than 0.7.[5]

Propellers

For a specific propeller geometry, Kt and Kq are often given as a function of the advance number J. It is a dimensionless number indicating some speed. It has all the components of how fast the rpm should be. These co-efficients are experimentally determined by so-called open water tests, usually performed in a cavitation tunnel or a towing tank.

Relation to tip speed ratio

The advance ratio is the inverse of the tip speed ratio, ${\displaystyle \lambda }$, used in wind turbine aerodynamics:[6]

${\displaystyle \mu =\lambda ^{-1}}$.

In operation, propellers and rotors are generally spinning, but could be immersed in a stationary fluid. Thus the tip speed is placed in the denominator so the advance ratio increases from zero to a positive non-infinite value as the velocity increases. Wind turbines use the reciprocal to prevent infinite values since they start stationary in a moving fluid.

See also

• Axial fan design
• Retreating blade stall
• Helicopter rotor
• Slowed rotor

Notes

1. Clancy, L.J. (1975), Aerodynamics, Section 17.2, Pitman Publishing Limited, London. ISBN 0-273-01120-0
2. Prof. Z. S. Spakovszky. "11.7.4.5 Typical propeller performance" MIT turbines, 2002. Thermodynamics and Propulsion, main page
3. Leishman, J. Gordon (2005). Principles of helicopter aerodynamics (2nd ed.). New York, NY: Cambridge University Press. ISBN 978-0-521-85860-1.
4. Jarugumilli, T.; Benedict, M.; Chopra, I. (1 May 2012). "Experimental Investigation of the Forward Flight Performance of a MAV-Scale Cycloidal Rotor". 68 Th Annual Forum and Technology Display of the American Helicopter Society.
5. Leishman, J. Gordon (2007). The helicopter : thinking forward, looking back. College Park, Md.: College Park Press. ISBN 978-0-9669553-1-6.
6. Spera, editor, David A. (2009). Wind turbine technology : fundamental concepts of wind turbine engineering (2nd ed.). New York, NY: ASME Press. ISBN 978-0791802601.CS1 maint: extra text: authors list (link)

External links

• Propeller Aircraft Performance and The Bootstrap Approach