1 in 60 rule
In air navigation, the 1 in 60 rule is a rule of thumb which states that if a pilot has travelled sixty miles then an error in track of one mile is approximately a 1° error in heading, and proportionately more for larger errors. The rule is used by single pilots with many other tasks to perform, often in a basic aircraft without the aid of an autopilot, who need a simple process that can be performed in their heads. This rule is also used by air traffic controllers to quickly determine how much to turn an aircraft for separation purposes.
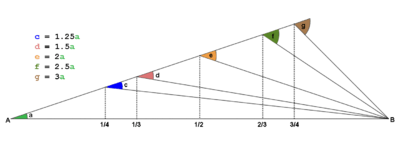
The rule is based on the small-angle approximation (which states that, for small angles, sin θ ≈ θ, where θ is in radians), along with the fact that one radian (which is about 57.3°) is close to 60°. In reality a 1 mile in 60 error is 0.96°, and the rule becomes increasingly inaccurate for larger errors. But since even a skilled pilot cannot manually fly with better than about 2° accuracy, and winds are constantly varying, the rule remains useful for most realistic situations.
This rule of thumb is incredibly powerful in the aviation environment. It states that for each degree off (or displacement) over a distance of 60 nautical miles (NM), it will result in 1 NM off course. It can be applied in various areas of interest when flying, and is easily remembered. This proves to be valuable in many different scenarios, en route navigation, approach, and even on vertical profiles.
The math behind this shows that this method is not entirely accurate, with roughly a 5% error, but the rule's objective is to get workable numbers in a dynamic environment, and it fits this purpose quite well. Here is the breakdown:
A circle of 60 NM radius has a circumference of:
2x60xπ = 376.99 NM
If we divide 376.99 by 360° we get:
376.99/360 = 1.047 NM (off by 4.7%)
We can consider this rule a very good approximation.
As a coincidence, 1 NM is about 6,000 feet (6,076.1 feet) so we can use the 60:1 rule for this too. For a 1 degree shift at 1 NM, there are about 100 feet of offset.
This becomes very useful for estimating or correcting vertical speed settings and flight path angles (FPA) during climb, descent, or approaches.
If a gradient in % is required, the numbers work out with the same rule:
1% over 1 NM ≈ 60'
It is also useful to find out the lateral deviation from a given VOR course or radial: Each dot on a VOR indicator represents 2° of deviation, or 200' per dot per DME.
There are other applications to this rule. One such application is time drift.
An hour is equal to 60 minutes, and a minute is equal to 60 seconds, so some other relationships between angle and time can be observed.
Examples
If a pilot is flying a leg of 120 miles and finds after traveling 60 miles that he is two miles to the right of track, then a correction of 4° to the left (2° to fly parallel to the intended track and another 2° to bring him to his target) will bring him to his destination.
If a pilot is flying a 120-mile leg and finds after 30 miles that he is two miles left of track, then he has flown 4° left of his intended track, i.e.
- 2 × 60/30
left of track. Changing the heading four degrees right will now bring him to parallel the intended track. At that point he still has 90 miles to his next waypoint. He is thus two miles to the left of that and thus the waypoint is 4/3 of a degree (2 × 60/90) to the right, or approximately 1° right. The pilot then adds these two to get 5° and flies 5° right of t his previous heading.
One can also use the 1 in 60 rule to approximate distance from a VOR, by flying 90 degrees to a radial and timing how long it takes to fly 10 degrees (the limit of the course deviation indicator). The time in seconds divided by 10 is roughly equal to the time in minutes from the station, at the current ground speed.
References
- Recreational Flying Enroute
- Taylor, Richard L., Fair Weather Flying, MacMillan 1981, p. 193, ISBN 0-02-616730-1
- Mike Roumens, "M3: The Mile, The Mach, The Minute, Mental Math For Aviators", pages 2–5, Copyright 2013, ISBN 1484846427
- https://www.cnatra.navy.mil/ebrief/documents/01_Training_Air_Wing_One/references/COLUMN%204/INST%20REFERENCES/60-1%20rules%20Jan%2007.pdf