11-cell

In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope (four-dimensional polytope). Its 11 cells are hemi-icosahedral, {3,5}/2. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol {(3,5)/2,3} or {{3,5}5,3}.

11-cell

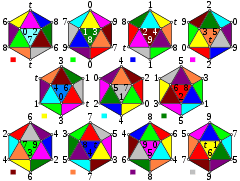The 11 hemi-icosahedra with vertices labeled by indices 0..9,t. Faces are colored by the cell it connects to, defined by the small colored boxes.
TypeAbstract regular 4-polytope
Cells11 {3,5}/2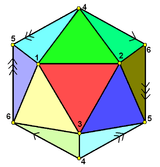
Faces55 {3}
Edges55
Vertices11
Vertex figure{5,3}/2
Schläfli symbol{(3,5)/2,3}
Symmetry group[(3,5)/2,3], order 660
Abstract L2(11)
Dualself-dual
PropertiesRegular

It has symmetry order 660, computed as the product of the number of cells (11) and the symmetry of each cell (60). The symmetry structure is the abstract group projective special linear group L2(11).

It was discovered in 1977 by Branko Grünbaum, who constructed it by pasting hemi-icosahedra together, three at each edge, until the shape closed up. It was independently discovered by H. S. M. Coxeter in 1984, who studied its structure and symmetry in greater depth.


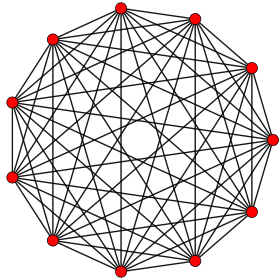
Orthographic projection of 10-simplex with 11 vertices, 55 edges.

The abstract 11-cell contains the same number of vertices and edges as the 10-dimensional 10-simplex, and contains 1/3 of its 165 faces. Thus it can be drawn as a regular figure in 11-space, although then its hemi-icosahedral cells are skew; that is, each cell is not contained within a flat 3-dimensional subspace.

gollark: My code waits `((length / 6000) / speed) - 2` seconds, then inefficiently checks the position of the tape every 0.05 seconds to see if it's hit the end.
gollark: I found that it reads 6000 bytes a second.
gollark: I'm not sure if it's that they're written to the tapes that way, or whether my code for determining the end of a track is a bit broken.
gollark: There's a weird issue where tracks cut off slightly early and I have no idea why, though. Better figure that out.
gollark: Is the label not limited in length?

See also

References
  • Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0
  • Coxeter, H.S.M., A Symmetrical Arrangement of Eleven hemi-Icosahedra, Annals of Discrete Mathematics 20 pp103–114.
  • The Classification of Rank 4 Locally Projective Polytopes and Their Quotients, 2003, Michael I Hartley
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.