0
Suppose one has functions f(i) and g(j). How could one write a function h(k), where the domain k of h is made up of all k=i+j (i.e., each point h(k) is some function of f at i and g at j for all pairs of i and j satisfying k=i+j). For instance:
for all k=i+j. The domain of h would thus be k=2:25 and, for instance, h(3) would be equal to f(1)*g(2) + f(2)*g(1) since both of these combinations satisfy k=i+j.
This is simple to do using loops, but I wish to compose the function in anonymous function form (i.e., h = @(k) f(i) ... g(j)). How can this be accomplished?
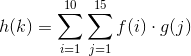
According to your formal example (with the sigma sums),
his constant. Want you actually want is an algorithm to find all valid sets ofi,jfor a givenk, such thatk=i+j. Sounds like a math problem. – jiggunjer – 2016-10-17T02:45:50.927