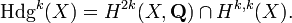Millennium Prize Problems

The Millennium Prize Problems are a set of seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. A correct solution to any of the problems results in a US$1,000,000 prize (popularly known in the mathematics world as a Millennium Prize) being awarded by the institute. The Clay Mathematics Institute, or CMI, is a private, non-profit foundation, based in Providence, Rhode Island.

Part of a convergent series on Mathematics

1+1=11

Drake equation Fermat Primes Gaussian distribution Information theory Littlewood's law Monkey typewriter theory Numbers Parallax method Pseudomathematics Seven Theresian mathematics Three v - t - e

As of 2015, six of the problems remain unsolved. The Poincaré conjecture is the single problem to be resolved, with a solution published by Grigori Perelman in 2003. Perelman was also awarded the Fields Medal (often called "the Nobel Prize of mathematics"), but he declined both awards, saying "I don't want to be on display like an animal in a zoo."[1] He felt equal credit was deserved by other mathematicians such as Richard Hamilton, whose methods he built upon.

The list of problems took inspiration from the Hilbert problems, a list of 23 problems presented by the German mathematician David Hilbert in 1900. The Millennium Prize Problems were presented in Paris in 2000 in the order given below. One of Hilbert's original problems, the Riemann hypothesis, is on the new list, and another, the Birch and Swinnerton-Dyer conjecture, follows on directly from the solution of the tenth Hilbert problem.

As exciting as the thought of winning a million bucks might be, if this is the first time you've heard of the Millennium Prizes, then there's a fairly strong chance you don't have the 10-15 years of formal mathematics study you'd probably need to even get started on solving one of these.

P versus NP

"P versus NP" is a (very 20th century) problem which emerged from computer science. The problem was introduced in 1971 by Stephen Cook in his paper "The complexity of theorem proving procedures"[2] and is considered by many to be the most important open problem in computer science.[3]

Obviously in order to understand the nature of the question, it is necessary to know what P and NP actually refer to. Both describe algorithms (repeating processes) which eventually reach a conclusion of some form.

First, consider a computer program that is capable of "verifying" an answer to a given problem. For example, assume the problem is: "From a list of one million randomly chosen numbers, find a list of 1000 numbers that add up to exactly one million". If you go then through the list and choose the required subset of 1000 numbers, the program will easily be able to verify whether or not your list adds up to one million (using simple arithmetic). There is a linear relationship between the number of members in the set (1000) and the number of steps required to solve the problem (1000 individual additions). A linear relationship is called a 'polynomial' relationship, so we will call these "answer verification" programs P.

Now consider the task of choosing the required subset of 1000 numbers in the first place. Currently there is no known way of quickly choosing all possible subsets; the only way to do so is through sheer brute force (i.e., testing every possible combination, of which there are 2ⁿ-1 possibilities). If you add another member to the subset, the number of solutions increases from 2ⁿ to 2ⁿ⁺¹, which is exponential or "non-polynomial" growth. We will call this "problem solving" program NP.

The P versus NP problem asks, is there some way of coming up with a nifty way of writing "problem solving" programs so that we can always avoid this "non-polynomial" growth? In other words, can there be a program that solves the problem in the same polynomial time as the verification program? If the answer is "yes", then 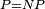. If the answer is "no", then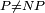

This is important because if 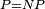then somewhere in "mathematics land" there is a quick and efficient way of cracking most encryption systems currently in use, including when you go to secure websites like your bank's. This is generally regarded as a "bad thing". On the plus side, most mathematicians are quite confident that 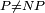. The problem is that no one knows how to prove it yet.

The Hodge conjecture

Some of the Millennium Problems defy easy description, and this is one of them.

The official statement of this problem is as follows: The Hodge conjecture asserts that for particularly nice types of spaces called projective algebraic varieties, the pieces called Hodge cycles are actually (rational linear) combinations of geometric pieces called algebraic cycles..[4]

In math jargon, this is:

So basically, unless you already know what a projective complex manifold is, and what cohomology means, there is no way you'll ever understand what this problem is even about.

Regardless, do let us know when you've solved it.

The Poincaré conjecture (solved)

The Poincare conjecture was an important conjecture in the field of topology, although its importance wasn't apparent at the time it was proposed. (As it has been proven, it's now technically a theorem.)

Topology is the mathematics of deformation; it considers surfaces independent of their dimensions. Hence, topologists are jokingly called "people who cannot tell the difference between a coffee cup and a donut" (because both are a continuous object with a single hole in the structure - see image).

The Poincaré conjecture involves a claim about objects in multi-dimensional space, and whether (under certain conditions) the object can be deformed to a sphere. Poincaré believed it to be true when he stated it in 1904. It wasn't regarded as a particularly important conjecture at the time, but it subsequently acquired great notoriety chiefly because on several occasions during the 20th century someone would claim they had solved the problem, only to later find a flaw.

By the 1980s all attempts to solve the problem had still failed, but had demonstrated that the problem had important implications in other areas of topology that Poincaré had never dreamed of. Hence it went from being an obscure comment in a 1904 paper to a major area of mathematical research.

The final solution was published online to arXiv in 2003 by a Russian mathematician named Grigori Perelman. After three years of intense scrutiny, his proof was accepted as definitive in 2006. How Perelman developed his thinking is a mystery as he refuses to talk to anyone, and there is speculation he may have ceased doing mathematics altogether. He was awarded the Fields Medal in 2006, and officially awarded the Millennium Prize in 2010, but he refused to accept both.

The Riemann hypothesis

The Riemann hypothesis was the eighth problem on Hilbert's list back in 1900, and it is still regarded as an important unsolved problem a century later. It is the only problem to appear on both lists.

A proof or disproof of this would have far-reaching implications in number theory, especially for the distribution of prime numbers. It also implies strong bounds on the growth of many other arithmetic functions.

The Riemann hypothesis concerns the properties of a mathematical function, the Riemann zeta function. The conjecture claims that all nontrivial zeros of the analytic continuation of the Riemann zeta function have a real part of 1/2.

Yang–Mills existence and mass gap

The Yang–Mills problem isn't so much a problem in mathematics as it is an open issue in mathematical physics.

It is fair to say that it is really complicated. Really, REALLY complicated. Regardless, here goes an attempt at a basic explanation.

We have quantum physics, which in the 1960s evolved into the Standard Model, and by the 1980s this had been refined to incorporate quantum field theory (QFT). One aspect of QFT is the existence of gauge particles which move back and forth between other particles, creating what we call "force".

The most widely accepted theoretical framework for explaining QFT is called Yang-Mills theory, and (among many other things) it predicts that the lightest gauge particles will still have mass. All experimental evidence seems to agree with this. (To help you understand the naming of the problem, the difference between the energy of the vacuum and the lightest particle is called the "mass gap".)

While this is all well and good, we're still a long way from being able to pin down what is exactly happening. The problem with QFT is it all happens in four (or more) dimensions, and there are dozens of different entities involved, so frankly, everyone is just a bit baffled. For an analogy, we're at the point in time where we know if we fire a catapult, the ball will land "over there somewhere", but we don't yet know calculus and so we aren't able to accurately predict where the ball will end up.

So solving this will be the quantum theory equivalent of developing calculus. The solution should also predict that the lightest gauge particles have mass.

Navier–Stokes existence and smoothness

Of the seven Millennium Prize problems, this has the most practical applications, particularly in resolving the issue of fluid turbulence.

The Navier–Stokes equations were developed in the 19th century and describe the motion of fluids. They are hugely important in many fields of engineering and applied science, since among other things both air and water are fluids. Air moving over a wing? Water moving through pipes? Ocean currents? Weather patterns? You can apply the Navier-Stokes equations to analyze these phenomena mathematically. Despite having been around for quite some time, they are still poorly understood. The problem is to make progress toward a mathematical theory that will give insight into these equations.

The official definition of the problem is: Prove or give a counter-example of the following statement: In three space dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier–Stokes equations.

The Birch and Swinnerton-Dyer conjecture

The Birch and Swinnerton-Dyer conjecture also has a long history. Hilbert's tenth problem dealt with a more general type of equation, and in that case it was proven that there is no way to decide whether a given equation even has any solutions.

This problem deals with a specific type of equation, those defining elliptic curves over the rational numbers. The conjecture is that there is a procedural way to determine whether such equations have a finite or infinite number of rational solutions.

References

1. Russian maths genius Perelman urged to take $1m prize bbc.co.uk, Wednesday, 24 March 2010.
2. Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.
3. Lance Fortnow, The status of the P versus NP problem, Communications of the ACM 52 (2009), no. 9, pp. 78–86. Template:Doi
4. Hodge Conjecture, Clay Mathematics Institute