Total aperiodic

A finite pattern is total aperiodic if it evolves in such a way that no cell in the plane is eventually periodic. The first example was found by Bill Gosper in November 1997. A few days later he found the much smaller example that consists of three copies of backrake 2 (by David Buckingham), shown to the right.

Total aperiodic
<html><div class="rle"><div class="codebox"><div style="display:none;"><code></html>x = 59, y = 57, rule = B3/S23 41bo$40b3o$39b2obo5bo$39b3o5b3o$40b2o4bo2b2o3b3o$46b3o4bo2bo$56bo$56bo $56bo$40b3o12bo$40bo2bo$40bo$40bo$41bo7$38b3o$38bo2bo11bo$38bo13b3o$ 38bo12b2obo$38bo12b3o$39bo12b2o3$35b3o$34b5o$34b3ob2o7b2o5bo2bo$37b2o 7b4o8bo$46b2ob2o3bo3bo$48b2o5b4o3$20bo$21bo$b2o13bo4bo32b3o$4o13b5o34b o$2ob2o51bo$2b2o51bo$36bo$37bo$21b2o10bo3bo$22b2o10b4o15b2o$21b2o27b3o b2o$21bo28b5o$51b3o2$22b2o$13b4o4b4o$12bo3bo4b2ob2o$b5o10bo6b2o$o4bo9b o$5bo$4bo! #C [[ THUMBSIZE 2 THEME 6 GRID GRIDMAJOR 0 SUPPRESS THUMBLAUNCH ]] <nowiki></nowiki> <html></code></div></div><canvas width="200" height="300" style="margin-left:1px;"><noscript></html> <html></noscript></canvas></div></html>
View static image
Pattern type Miscellaneous
Number of cells 182
Bounding box 59×57
Discovered by Bill Gosper
Year of discovery 1997

On June 24, 2004, Gosper found that a block can be added to the pattern to make the total periodic pattern shown below, in which every cell eventually becomes periodic (albeit incredibly slowly). The block remains untouched for about 363 generations. It deletes its nth glider (and is shifted) at about generation 357.5+5.5n.[1]

Total periodic
RLE: here
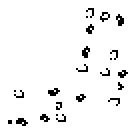gollark: OIR™ has one.
gollark: How did it do *that*?
gollark: ++remind 2h fix
gollark: ++magic reload_ext irc_link
gollark: How does it keep *doing* that?

References
  1. Jason Summers' jslife oversize pattern collection.
This article is issued from Conwaylife. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.