Moore neighbourhood

The Moore neighbourhood is the set of all cells that are orthogonally or diagonally-adjacent to the region of interest (the region of interest itself may or may not be considered part of the Moore neighbourhood, depending on context). For example, the Moore neighbourhood of a single cell consists of the eight cells immediately surrounding it. This neighbourhood is named after Edward F. Moore, one of the pioneers of cellular automata theory.[1] The Moore neighborhood is the neighbourhood of interest in Conway's Game of Life and all Life-like cellular automata, though there are cellular automata that use other neighbourhoods such as the 4-cell von Neumann neighborhood.

The Moore neighbourhood (in green) of a single cell

The Moore neighbourhood naturally extends to cellular automata in higher dimensions, for example forming a 26-cell cubic neighborhood for a cellular automaton in three dimensions. The number of cells in the Moore neighbourhood of a single cell in an n-dimensional cellular automaton is 3n-1 (Sloane's  A024023 ).

The Moore neighbourhood of a cell can be thought of as the points at a Chebyshev distance of 1 from that cell.

Generalizations
Main article: Isotropic non-totalistic Life-like cellular automaton

Like in the hexagonal neighborhood, isotropic cellular automata using the Moore neighbourhood can be defined using Hensel notation, which was devised by Alan Hensel and represents the relative permutations of the cells using letters.

012345678
— (no
letter)
c
(corner)
e
(edge)
k
(knight)
a
(adjacent)
i
n
y
q
j
r
t
w
z

For instance, B2-a/S12 (the Just Friends rule) indicates that a dead cell will be born with 2 neighbors, except when they are adjacent, and that a live cell will survive with 1 or 2 neighbors in any configuration.

Higher ranges

The Moore neighbourhood can also be defined with a higher range; that is, so that it captures cells that are further than one cell away from the region of interest. The standard Moore neighbourhood has range 1. The Moore neighbourhood of range 2 is the set of all cells that are orthogonally or diagonally-adjacent to the Moore neighbourhood itself. The Moore neighbourhood of range n can be defined recursively as the set of all cells that are orthogonally or diagonally-adjacent to the Moore neighbourhood of range n-1. The number of cells in the Moore neighbourhood of range n is given by (2n+1)2-1 (Sloane's  A033996 ).

Symmetries
Main article: Symmetry

The Moore and von Neumann neighbourhoods rely on a different grid than the hexagonal neighbourhood and thus features a different set of inherent symmetries when dealing with isotropic rules:

  • C2_1
  • C2_2
  • C2_4
  • C4_1
  • C4_4
  • D2_+1
  • D2_+2
  • D2_x
  • D4_+1
  • D4_+2
  • D4_+4
  • D4_x1
  • D4_x4
  • D8_1
  • D8_2 (only occasionally preserved)
  • D8_4
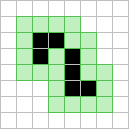The Moore neighbourhood (in green) of an eater 1
The Moore neighbourhood of range 2 of a single cell
The Moore neighbourhood of range 3 of a single cell
gollark: Destroy a computer?W hat?
gollark: So what exactly does that help with?
gollark: https://cdn.discordapp.com/attachments/477911902152949771/636636449151909900/unknown.png
gollark: `OperatingSystem_ON` is a giveaway.
gollark: "OS"ey, I mean.

See also

References
  1. Tim Tyler. "The Moore neighbourhood". Retrieved on June 13, 2009.
This article is issued from Conwaylife. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.