12
1
Introduction
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots are thought of as alphas (units). These are one type of 2-dimensional figurate numbers.
The number 10, for example, can be arranged as a triangle:
* ** *** ****But 10 cannot be arranged as a square. The number 9, on the other hand, can be:
*** *** ***Some numbers, like 36, can be arranged both as a square and as a triangle:
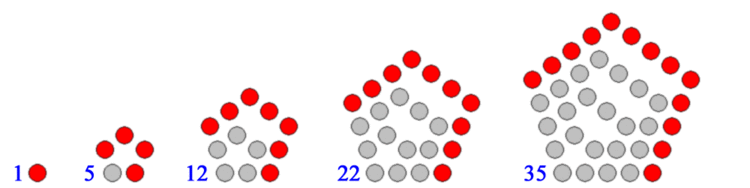
****** * ****** ** ****** *** ****** **** ****** ***** ****** ******By convention, 1 is the first polygonal number for any number of sides. The rule for enlarging the polygon to the next size is to extend two adjacent arms by one point and to then add the required extra sides between those points. In the following diagrams, each extra layer is shown as in red.
Triangular Numbers:
Square Numbers:
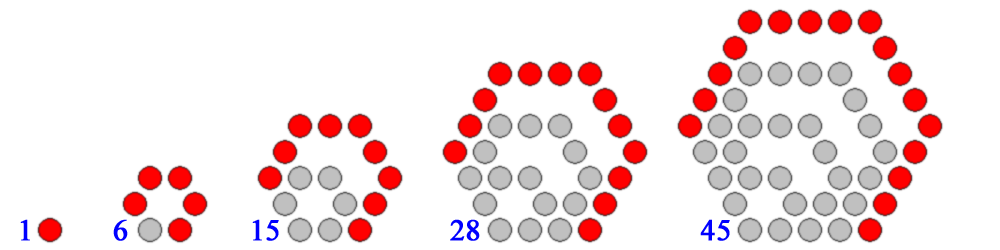
Polygons with higher numbers of sides, such as pentagons and hexagons, can also be constructed according to this rule, although the dots will no longer form a perfectly regular lattice like above.
Pentagonal Numbers:
Hexagonal Numbers:
Source: Wikipedia
Your task
Given a positive integer N (1 <= N <= 1000), print every type of Polygonal Number N is starting from Triangular Numbers up to and including Icosagonal (20-gon) Numbers.
For example, the number 10 is a triangular number and a decagonal number, so the output should be something like (you can choose your own output format, but it should look somewhat like this):
3 10
Test cases
1 -> 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 -> (None)
3 -> 3
6 -> 3 6
36 -> 3 4 13
For reference, the n-th k-gonal number is:
Credit: xnor
Remember, this is code-golf, so the code with the fewest bytes wins.


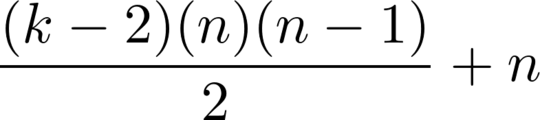
For reference, the
nth k-gonal number is(k-2)*n*(n-1)/2 + n. – xnor – 2016-11-13T23:41:42.1878The point of the sandbox is to improve questions. If you post a question in the sandbox and discover that it's not clear what you're asking, the correct response is not to add a comment in the sandbox, wait two hours, and then post the question to main unmodified and delete the sandbox question, hiding the explicatory comment from people with less than a couple of thousand rep. The correct response is to rephrase or ask for suggestions for rephrasing, and give it another day or two to see whether the rephrased question still has problems. – Peter Taylor – 2016-11-14T07:37:50.120