21
Using the the ten inferences of the Natural Deduction System prove DeMorgan's laws.
The Rules of Natural Deduction
Negation Introduction:
{(P → Q), (P → ¬Q)} ⊢ ¬PNegation Elimination:
{(¬P → Q), (¬P → ¬Q)} ⊢ PAnd Introduction:
{P, Q} ⊢ P ʌ QAnd Elimination:
P ʌ Q ⊢ {P, Q}Or Introduction:
P ⊢ {(P ∨ Q),(Q ∨ P)}Or Elimination:
{(P ∨ Q), (P → R), (Q → R)} ⊢ RIff Introduction:
{(P → Q), (Q → P)} ⊢ (P ≡ Q)Iff Elimination:
(P ≡ Q) ⊢ {(P → Q), (Q → P)}If Introduction:
(P ⊢ Q) ⊢ (P → Q)If Elimination:
{(P → Q), P} ⊢ Q
Proof structure
Each statement in your proof must be the result of one of the ten rules applied to some previously derived propositions (no circular logic) or an assumption (described below). Each rule operates across some propositions on the left hand side of the ⊢ (logical consequence operator) and creates any number of propositions from the right hand side. The If Introduction works slightly differently from the rest of the operators (described in detail below). It operates across one statement that is the logical consequent of another.
Example 1
You have the following statements:
{(P → R), Q}
You may use And Introduction to make:
(P → R) ʌ Q
Example 2
You have the following statements:
{(P → R), P}
You may use If Elimination to make:
R
Example 3
You have the following statements:
(P ʌ Q)
You may use And Elimination to make:
P
or to make:
Q
Assumption Propagation
You may at any point assume any statement you wish. Any statement derived from these assumptions will be "reliant" on them. Statements will also be reliant on the assumptions their parent statements rely on. The only way to eliminate assumptions is by If Introduction. For If introduction you start with a Statement Q that is reliant on a statement P and end with (P → Q). The new statement is reliant on every assumption Q relies on except for assumption P. Your final statement should rely on no assumptions.
Specifics and scoring
You will construct one proof for each of DeMorgan's two laws using only the 10 inferences of the Natural Deduction Calculus.
The two rules are:
¬(P ∨ Q) ≡ ¬P ʌ ¬Q
¬(P ʌ Q) ≡ ¬P ∨ ¬Q
Your score is the number of inferences used plus the number of assumptions made. Your final statement should not rely on any assumptions (i.e. should be a theorem).
You are free to format your proof as you see fit.
You may carry over any Lemmas from one proof to another at no cost to score.
Example Proof
I will prove that (P and not(P)) implies Q
(Each bullet point is +1 point)
Assume
not (Q)Assume
(P and not(P))Using And Elim on
(P and not(P))derive{P, not(P)}Use And Introduction on
Pandnot(Q)to derive(P and not(Q))Use And Elim on the statement just derived to make
P
The new P proposition is different from the other one we derive earlier. Namely it is reliant on the assumptions not(Q) and (P and not(P)). Whereas the original statement was reliant only on (P and not(P)). This allows us to do:
If Introduction on
Pintroducingnot(Q) implies P(still reliant on the(P and not(P))assumption)Use And Introduction on
not(P)andnot(Q)(from step 3) to derive(not(P) and not(Q))Use And Elim on the statement just derived to make
not(P)(now reliant onnot(Q))If Introduction on the new
not(P)introducingnot(Q) implies not(P)We will now use negation elimination on
not(Q) implies not(P)andnot(Q) implies Pto deriveQ
This Q is reliant only on the assumption (P and not(P)) so we can finish the proof with
- If Introduction on
Qto derive(P and not(P)) implies Q
This proof scores a total of 11.
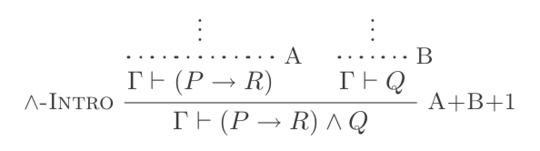
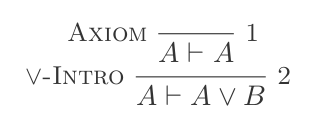
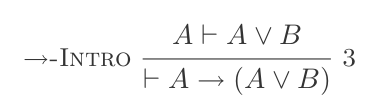
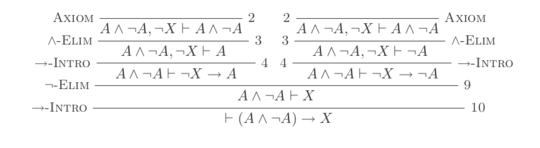
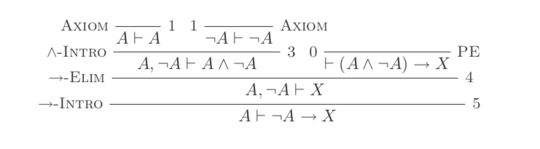
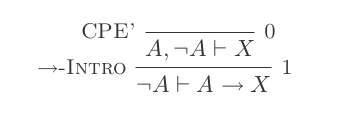

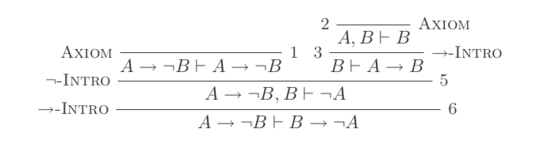

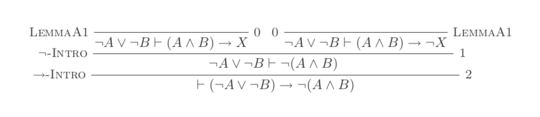
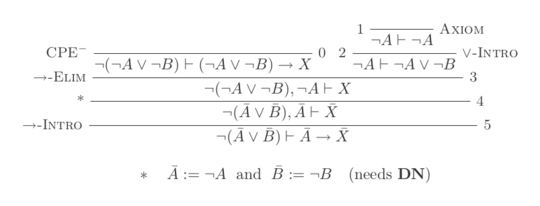
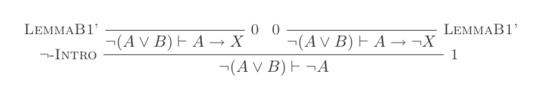
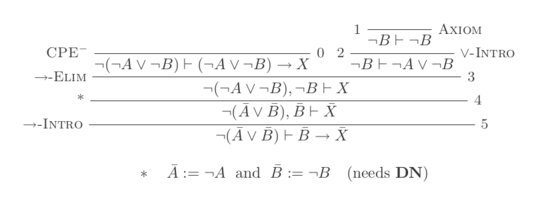
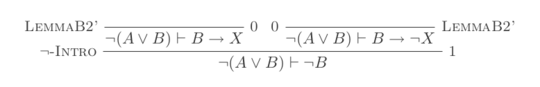
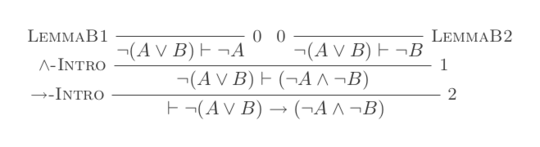
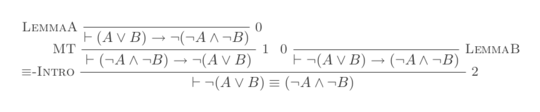
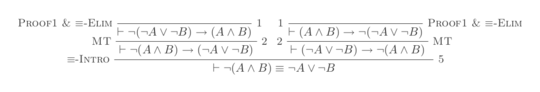
7
Although the consensus on meta is clear, not everyone will have seen it yet, so this is just to highlight that proof golfing is on topic.
– trichoplax – 2016-10-16T08:33:01.3132I think you should explain the structure of proofs and
⊢(the symbol also doesn't render for me on mobile). – xnor – 2016-10-16T08:39:02.6033I think the explanations definitely help. What I'd find most useful would a worked and scored example of some simple proof that includes If-Introduction and assumptions, preferably nested. Maybe of contrapositive? – xnor – 2016-10-16T09:02:35.900
1In your example, I believe that the first two assumptions would have to be flipped; nowhere does it state that
(P ⊢ (Q ⊢ R)) ⊢ (Q ⊢ (P ⊢ R))(in this instance,¬Q ⊢ ((P ʌ ¬P) ⊢ P)to(P ʌ ¬P) ⊢ (¬Q ⊢ P)was used). – LegionMammal978 – 2016-10-16T12:40:23.277@LegionMammal978 the order of assumptions does not matter. The ⊢ operator is transitive. – Post Rock Garf Hunter – 2016-10-16T16:29:00.397
@Dennis will just make a Jelly builtin and have an infinite score haha. – Buffer Over Read – 2016-10-17T00:58:54.390
@TheBitByte Dennis should definitely make a Jelly builtin, but given the rules of the site he will have no score – edc65 – 2016-10-17T07:03:46.777
@WheatWizard You should still state that
(P ⊢ (Q ⊢ R)) ⊢ (Q ⊢ (P ⊢ R)); additionally, I can't see how you got from step 6 to step 7. – LegionMammal978 – 2016-10-17T11:33:52.343@LegionMammal978 I see your confusion. Step 7 does not follow from step 6 but rather follows from step 3. The proof is not quite linear. I will try to make this clearer – Post Rock Garf Hunter – 2016-10-17T15:21:43.500
I don't understand this reliance business. For example, @feersum's proof contains
assume ~P { Q ^ Q; Q; } ~P -> Qbut isn'tQsupposed to rely onPfor this to work? – Neil – 2016-10-19T09:12:05.970@Neil I am not sure I understand feersum's proof myself. I am working on verifying it right now but I am having particular trouble with the portion you mention. However it is perfectly fine for something to rest on two contradictory assumptions. – Post Rock Garf Hunter – 2016-10-19T11:48:07.217
The first 2 are equivalent... because if i have one axiom formula f(a,b,c) where a b c are proposition variables than f(not a, b, c) f(a, not b, c)... f(not a, not b, not c) should be true too... – RosLuP – 2016-10-19T15:20:42.967
@RosLuP While your assertion is in fact true it is actually a consequent of the second axiom. While these two axioms may seem trivially redundant, since we do not have
~(~P) -> Pand cannot prove it without axiom 2 the two axioms are in fact both required. – Post Rock Garf Hunter – 2016-10-19T15:24:57.4831Are you allowed to prove multiple things in a single "assumption context", and then extract multiple implication statements, to save on how many "assumption lines" are needed? e.g.
(assume (P/\~P); P,~P by and-elim; (assume ~Q; P by assumption; ~P by assumption); ~Q->P by impl-intro; ~Q->~P by impl-intro; Q by neg-elim); P/\~P->Q by impl-introto get a score of 9? – Daniel Schepler – 2017-10-02T22:37:09.213Also, I don't see an "assumption" rule, so I'm not sure how you actually prove
P -> P. Would a proof like1. assume P; 2. P -> P by impl-intro, 1, 1be acceptable? Or, to proveP -> P /\ P: would1. { assume P; 2. P /\ P by and-intro, 1, 1 }; 3. P -> P /\ P by impl-intro, 1, 2be acceptable? – Daniel Schepler – 2017-10-03T00:00:51.840