43
8
An aesthetically pleasing divisor tree is a tree of divisors of input n that, for any composite number m, has two children nodes that are the pair of divisors that are closest to the square root of m. The left node should be the smaller divisor of m and the right node should be the larger divisor of m. A prime number in the tree should have no children nodes. Your tree may be in the form of text art or an image. The rules for text art output are as follows.
Spacing rules
To space out the nodes on the tree, we have the following rules:
- The nodes at a given depth from the root should all be on the same line of text in the output.
/ \ NOT / \ / \ / 3 2 3 2
- For left nodes, the incoming branch should be on the upper right if the node is a single-digit number, else, just above the last digit. Example:
/ AND / 3 720
- For right nodes, the incoming branch should be on the upper left if the node is a single-digit number, else, just above the first digit. Example:
\ AND \ 7 243
- For outgoing left branches, the branch should begin one space to the left of the number. Example:
275 / 11
- For outgoing right branches, the branch should begin one space to the right of the number. Example:
275 \ 25
- Any two nodes on the same level of the tree should have a minimum of two spaces between them. At the same time, any two subtrees on the same level of the tree should have as few spaces between them as possible.
This tree doesn't work because the **subtrees** are too close.
504
/ \
/ \
/ \
/ \
21 . 24
/ \ . / \
/ \ . / \
3 7. 4 6
. / \ / \
.2 2 2 3
While this tree does have enough space between its branches.
504
/ \
/ \
/ \
/ \
/ \
21 ... 24
/ \ ... / \
/ \ ... / \
3 7... 4 6
... / \ / \
...2 2 2 3
- If any two subtrees are too close together on a tree, they can be separated by adding another row of branches
/\to the tree above the parents.
441
/ \ Last row is not filled in yet and we have already run out of space.
21 21
/ \ / \
Add another row of branches
441
/ \ Almost, but the 7 and the 3 are too close together.
/ \ One more row should do it.
21 21
/ \ / \
3 7 3 7
Add another row of branches
441
/ \ And we're done.
/ \
/ \
21 21
/ \ / \
3 7 3 7
Examples
As a full example, the divisor tree of 24 will look like this:
24
/ \
/ \
4 6
/ \ / \
2 2 2 3
4 and 6 are the pair of divisors closest to the square root of 24. 4 is on the left, because it's smaller. On the next line, the number 2 to the left of 3, because it's smaller.
The divisor tree for 63 should look like:
63 and NOT like this 63
/ \ / \
7 9 3 21
/ \ / \
3 3 7 3
In the incorrect tree, 3 and 21 are not the pair of divisors closest to the square root of 63, and 3 and 7 are not sorted properly. The branch placement on the 21 is correct, though.
For 42, you should have:
42 and NOT 42
/ \ / \
6 7 21 2
/ \ / \
2 3 3 7
Let's have a look at 720. Note that we need five levels of branches from 720 so that the 24 and 30 subtrees are correctly spaced. Also, note that 24 and 30 have two levels of branches because 4 and 6 have children nodes that need correct spacing and the children nodes of 30 need to be on the same level as the children nodes of 24.
720
/ \
/ \
/ \
/ \
/ \
24 30
/ \ / \
/ \ / \
4 6 5 6
/ \ / \ / \
2 2 2 3 2 3
The challenge
- Your task is to build a correctly-spaced aesthetically pleasing divisor tree for input
n, wherenis a positive integer greater than 1. - Your output may contain leading and trailing spaces and leading and trailing newlines, but must otherwise conform to the spacing rules given above.
- Your output is allowed to be: text art, an image (other formats to be added, if needed).
- For images, make sure your tree's nodes are well-spaced, and that nodes at the same height in the tree are at the same height in the image.
- This is code golf. Least number of bytes (or equivalent) wins.
Credit to Stewie Griffin for thinking of this idea, and many thanks to Peter Taylor, Martin Ender, Mego, and Eᴀsᴛᴇʀʟʏ Iʀᴋ for their help in rewriting the specification. As usual, any suggestions or corrections are much appreciated. Good luck and good golfing!
More test cases:
2
4
/ \
2 2
20
/ \
4 5
/ \
2 2
323
/ \
17 19
362880
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
576 630
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
24 24 21 30
/ \ / \ / \ / \
/ \ / \ / \ / \
4 6 4 6 3 7 5 6
/ \ / \ / \ / \ / \
2 2 2 3 2 2 2 3 2 3
1286250
/ \
/ \
/ \
/ \
/ \
1050 1225
/ \ / \
/ \ / \
/ \ / \
30 35 35 35
/ \ / \ / \ / \
5 6 5 7 5 7 5 7
/ \
2 3
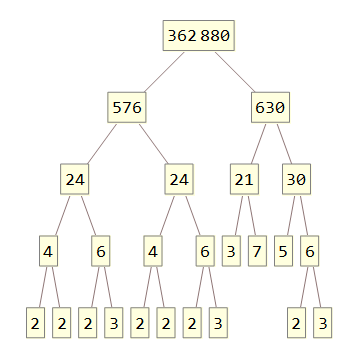
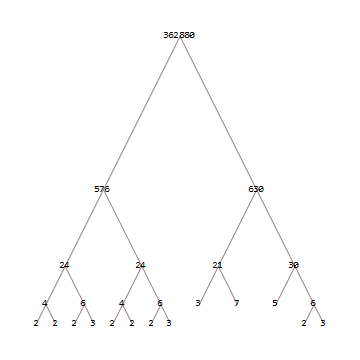
Thank you for this challenge. I can now visualize these things without drawing them each time :D – Conor O'Brien – 2016-10-01T15:22:39.407
Does the tree need to look like the examples, or can I use the built-in Mathematica function? It looks like this, but with factorization.
– JungHwan Min – 2016-10-01T15:40:18.720@JHM I knew I should have kept the [tag:graphical-output] tag. Yes, you may use that built-in. I'll edit the challenge. – Sherlock9 – 2016-10-01T16:03:34.347