21
13
Execute a Lindenmayer System
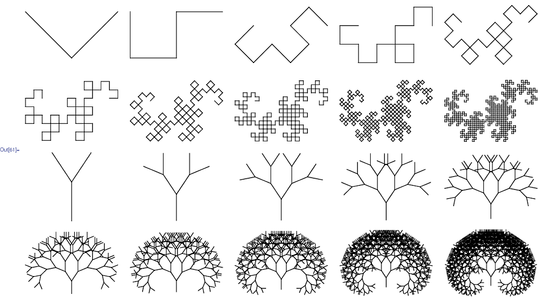
A Lindenmayer System (or L-system) is related to Thue and Post systems, and is used in botanical modeling and fractal generation.
An L-system is described by string-rewriting where a symbol from the symbol-alphabet is mapped to a replacement sequence of symbols. A collection of these mappings constitutes the L-system proper.
The graphical output method as devised by Prusinkiewicz interprets the resulting sequence after the mappings have been applied to an initial sequence for a specified number of iterations, as Turtle-Drawing commands: forward, backward, left, right, that kind of stuff. This may require extra code to control the scale of the drawing as different iteration counts may produce drastically differently-sized images.
Your task is to execute an L-system in the fewest number of characters. Your program must be able to render both the Dragon Curve and the Branching Stems from the Wikipedia page by providing appropriate input (file, command-line, but external to the source, please).
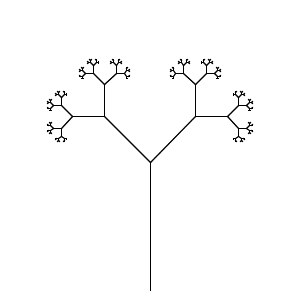

This is code golf.
Edit: Here are some examples I've posted around town. answer to SO/rotate-to-north {Where I first discovered the L-system}, answer to SO/how-to-program-a-fractal, answer to SO/recursion-in-postscript, comp.lang.postscript discussion/recital, postscript l-system collection, codegolf.SE/draw-a-sierpinski-triangle {origin of the competition between myself and thomasW}.


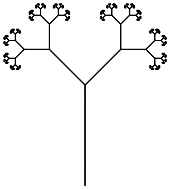


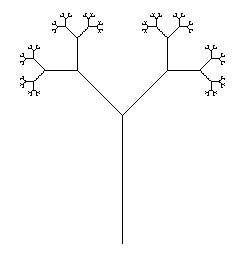



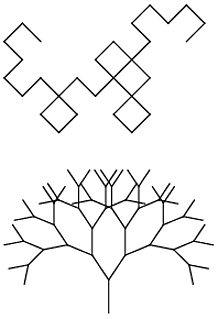
Skipped the sandbox. This seems relatively straightforward and should be fun. – luser droog – 2012-12-31T11:32:53.603
BTW, anybody know the origin of the above quote? I've heard William James, and I've heard Faraday. – luser droog – 2012-12-31T11:57:42.770
1Wikipedia says the origin is in dispute, best guess is Bertrand Russel. – ugoren – 2012-12-31T13:09:35.277
ITYM Bertrand Russell. – Paul R – 2012-12-31T16:06:39.713
1Are there any limits on the size of the alphabet, number of rules, number of rounds or possible (visualization) rules (draw a straight line, push/pop position/angle, turn how many degrees etc.) If we only need to draw those two then we would need pushing & popping, drawing straight lines and being able to turn 45 degrees in both directions, only two rules and an alphabet of size 4. – shiona – 2012-12-31T16:54:44.863
@shiona The hope is that it would draw more than these two. But if you can make simplifying assumptions that hold for these two, that's ok. – luser droog – 2012-12-31T17:18:54.610
Wait a moment ... I think it may actually be Max Müller. I was reading a fax of his Theosophy not too long ago.
– luser droog – 2013-01-01T04:09:09.420@shiona Did I answer your question? – luser droog – 2013-01-29T09:07:34.457
@luserdroog yes – shiona – 2013-01-29T14:02:49.397