Quixels - Quantum Pixels

Question

Introduction

A quixel is a quantum pixel. Similar to a classical pixel, it is represented with 3 integer values (Red, Green, Blue). However, quixels are in a super position of these 3 states instead of a combination. This super position only lasts until the quixel is observed at which point it collapses to one of three classical pixels; RGB(255,0,0), RGB(0,255,0) and RGB(0,0,255).

Specification

• Representation
  • Each quixel is represented as an array of 3 integers between 0 and 255, r, g and b respectively.
• Super Positions
  • Each quixel is in a super position between the Red, Blue and Green states represented by R, G and B respectively.
• Observation
  • When each quixel is observed it collapses into one of the three states. The probability of each classical state is R = (r + 1) / (r + g + b +3), G = (g + 1) / (r + g + b + 3) and B = (b + 1) / (r + g + b + 3). This way each classical state always as a non-zero probability of showing up.
• Input
  • The function or program should take a image of quixels. How it does this is flexible. A filename, using a multi-dimensional array, etc are all acceptable.
• Output
  • The function or program should produce an image of classical pixels. The data structure for this produced image is also flexible. Note that all of the pixels should be one of these three: RGB(255,0,0), RGB(0,255,0) and RGB(0,0,255)
  • The output should not be deterministic; these are quantum pixels! The same input should result in different outputs.
  • If your language has no way of generating a random number, you can take random bytes as input
• Scoring
  • This is code-golf so fewest bytes win.

---

Images

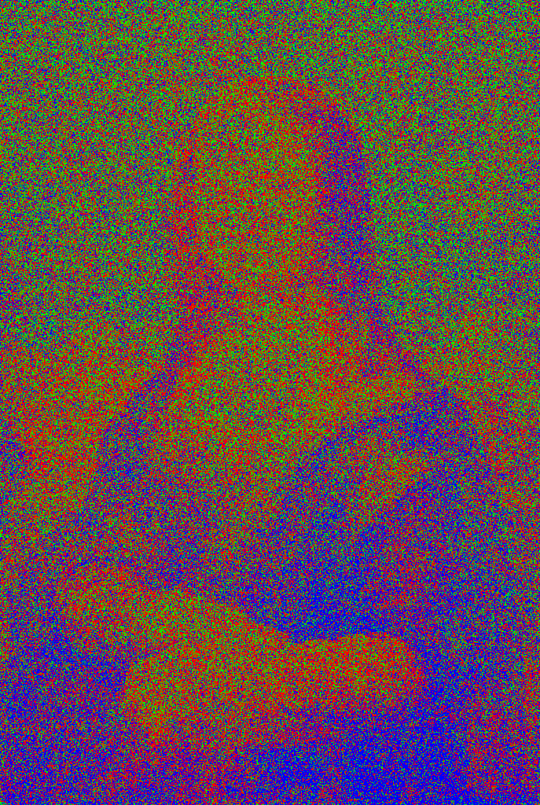
Mona Lisa by Leonardo da Vinci

Starry Night by Vincent van Gogh

Persistence of Memory by Salvador Dali

Teddy Roosevelt VS. Bigfoot by SharpWriter

Answer 1

Dyalog APL, 23 21 19 bytes

Takes table of (R, G, B) triplets.

Inspired by miles' algorithm

Returns table of indices into {(255, 0, 0), (0, 255, 0), (0, 0, 255)}. Horribly wasteful.

(?∘≢⊃⊢)¨(⊂⍳3)/¨⍨1+⊢

(
 ?∘≢ random index
 ⊃ selects
 ⊢ from
)¨ each of

(
 ⊂ the entire
 ⍳3 first three indices
)/¨⍨ replicated by each of

1+⊢ the incremented triplets

TryAPL!

---

Old version

Returns table of 0-based indices into {(255, 0, 0), (0, 255, 0), (0, 0, 255)}

{+/(?0)≥+\(1+⍵)÷3++/⍵}¨

{...}¨ for each quixel in the table, find the:

 +/ the sum of (i.e. count of truths of)

 (?0)≥ a random 0 < number < 1 being greater than or equal to

 +\ the cumulative sum of

 (1+⍵)÷ the incremented RGB values divided by

 3+ three plus

 +/⍵ the sum of the quixel

Note: Dyalog APL lets you chose between the Lehmer linear congruential generator, the Mersenne Twister, and the Operating System's RNG¹ ².

For example, the image:

┌──────────┬──────────┬───────────┬───────────┬─────────┐
│52 241 198│148 111 45│197 165 180│9 137 120  │46 62 75 │
├──────────┼──────────┼───────────┼───────────┼─────────┤
│81 218 104│0 0 255   │0 255 0    │181 202 116│122 89 76│
├──────────┼──────────┼───────────┼───────────┼─────────┤
│181 61 34 │84 7 27   │233 220 249│39 184 160 │255 0 0  │
└──────────┴──────────┴───────────┴───────────┴─────────┘

can give

┌─┬─┬─┬─┬─┐
│1│0│2│2│1│
├─┼─┼─┼─┼─┤
│2│2│1│1│2│
├─┼─┼─┼─┼─┤
│0│2│1│2│0│
└─┴─┴─┴─┴─┘

Notice how the three "pure" quixels collapsed to their respective colors.

TryAPL online!

Answer 2

Mathematica, 53 bytes

RandomChoice[255#+1->IdentityMatrix@3]&~ImageApply~#&

Anonymous function. Takes a Mathematica Image as input and returns an Image as output. Note that the input image must have an RGB color space.

Answer 3

C#, 366 243 bytes

Huge thanks to @TheLethalCoder for golfing this!

var r=new Random();c=>{double t=c.R+c.G+c.B+3,x=(c.R+1)/t,d=r.NextDouble();return d<=x?Color.Red:d<=x+(c.G+1)/t?Color.Lime:Color.Blue;};b=>{fo‌​r(int x=0,y;x<b.Width;x++)for(y=0;y<b.Height;y++)b.SetPixel(x,y,g(‌​b.GetPixel(x,y)));re‌​turn b;};

Basic idea:

using System;
using System.Drawing;
static Random r = new Random();

static Image f(Bitmap a) {
    for (int x = 0; x < a.Width; x++) {
        for (int y = 0; y < a.Height; y++) {
            a.SetPixel(x, y, g(a.GetPixel(x, y)));
        }
    }
    return a;
}

static Color g(Color c) {
    int a = c.R;
    int g = c.G;
    double t = a + g + c.B + 3;
    var x = (a + 1) / t;
    var y = x + (g + 1) / t;
    var d = r.NextDouble();
    return d <= x ? Color.Red : d <= y ? Color.Lime : Color.Blue;
}

---

Examples:

Mona Lisa

Starry Night

Persistence of Memory

Teddy Roosevelt VS. Bigfoot

Here's an updated imgur album with a few more examples, to show that this is nondeterministic.

Answer 4

Python 2, 172 166 162 bytes

The second and third indent levels are a raw tab and a raw tab plus a space, respectively; this plays really badly with Markdown, so the tabs have been replaced by two spaces.

from random import*
i=input()
E=enumerate
for a,y in E(i):
 for b,x in E(y):
  t=sum(x)+3.;n=random()
  for j,u in E(x):
   n-=-~u/t
   if n<0:i[a][b]=j;break
print i

Uses a similar input/output format to Adám's APL answer. Input is a 2D array of RGB tuples; output is a 2D array of 0, 1, or 2, representing red, green, and blue respectively. For example:

$ echo "[[(181,61,34),(39,184,160),(255,0,0)],[(84,7,27),(123,97,5),(12,24,88)]]" | python quixel.py
[[2, 2, 0], [0, 0, 0]]

Below is my older Python 3 answer using PIL.

Python 3 + PIL, 271 250 245 243 bytes

import random as a,PIL.Image as q
i=q.open(input())
w,h=i.size
for k in range(w*h):
 m=k//h,k%h;c=i.getpixel(m);t=sum(c)+3;n=a.random()
 for j,u in enumerate(c):
  n-=-~u/t
  if n<0:z=[0]*3;z[j]=255;i.putpixel(m,tuple(z));break
i.save('o.png')

Iterates over every pixel and applies the quixel function to it. Takes the filename as input and saves its output in o.png.

Here are some results:

$ echo mona-lisa.jpg | python quixel.py

$ echo starry-night.jpg | python quixel.py

$ echo persistence-of-memory.jpg | python quixel.py

$ echo roosevelt-vs-bigfoot.jpg | python quixel.py

Answer 5

J, 20 18 17 bytes

(>:({~?@#)@##\)"1

The image is input as an array with dimensions h x w x 3 representing the RGB values as integers in the range 0 - 255. The output is a table with dimensions h x w where 1 is an rgb value of (255, 0, 0), 2 is (0, 255, 0), and 3 is (0, 0, 255).

Explanation

The ()"1 represents that this verb is to be applied to each array of rank 1 in the input, meaning that it will apply to each pixel.

>:({~?@#)@##\  Input: array [R G B]
>:             Increment each, gets [R+1, G+1, B+1]
           #\  Gets the length of each prefix of [R G B], forms [1 2 3]
          #    Make a new array with R+1 copies of 1, G+1 copies of 2,
               and B+1 copies of 3
  (     )@     Operate on that array
       #         Get the length of the array of copies, will be R+G+B+3
     ?@          Generate a random integer in the range [0, R+G+B+3)
   {~            Select the value at that index from the array of copies and return

Answer 6

R, 58 bytes

mapply(function(r,g,b)rmultinom(1,1,c(r+1,g+1,b+1)),r,g,b)

Input consists of three numeric vectors held in r, g and b respectively.

We don't need to normalise the probabilities to sum to one, that happens automatically in rmultinom.

Output is of the form

     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]    0    0    0    0    0    0    0    0    0     0
[2,]    0    0    0    1    0    0    1    1    1     0
[3,]    1    1    1    0    1    1    0    0    0     1

Where there is a single 1 in each column. The 1 is in the first row for "R" pixels, the second row for "G" and the third row for "B".

Answer 7

Jelly, 8 7 bytes

Jx‘Xµ€€

The input is a 3d list with dimensions h x w x 3. The output is a 2d list with dimensions h x w where 1 represents the rgb value (255, 0, 0), 2 is (0, 255, 0), and 3 is (0, 0, 255).

The sample input below is the top-left 4 x 4 region of the Mona Lisa image.

Try it online!

Explanation

Jx‘Xµ€€  Input: The 3d list of rgb pixels
    µ    Begin a monadic chain (Will operate on each pixel, input: [R, G, B])
J          Enumerate indices to get [1, 2, 3]
  ‘        Increment each to get [R+1, G+1, B+1]
 x         Make R+1 copies of 1, G+1 copies of 2, B+1 copies of 3
   X       Select a random value from that list of copies and return
     €€  Apply that monadic chain for each list inside each list

Answer 8

Pyth - 11 10 bytes

Takes RGB 2d bitmap and outputs bitmap with indexed 3-bit color.

mLOs.emkbk

That level of nesting is hurting my head.

Try it online here.

Answer 9

Python 3, 119 bytes

Where m is the input taken as a 2-d array of pixels where each pixel is a list of the form [r,g,b]. At each pixel's position, returns 0,1,2 to represent (250,0,0), (0,250,0), and (0,0,250) respectively.

import random
lambda m:[map(lambda x:x.index(sum((((i+1)*[i])for i in x),[])[random.randint(0,sum(x)+2)]),i)for i in m]