Normal distribution values

7

1

Write the shortest program possible which outputs a table of Normal distribution values 

phi(z) = Integral[t from -infty to z of e^(-t^2/2) /sqrt(2 pi) dt]

for z from 0.00 to 3.99, giving values accurate to 4 decimal places.

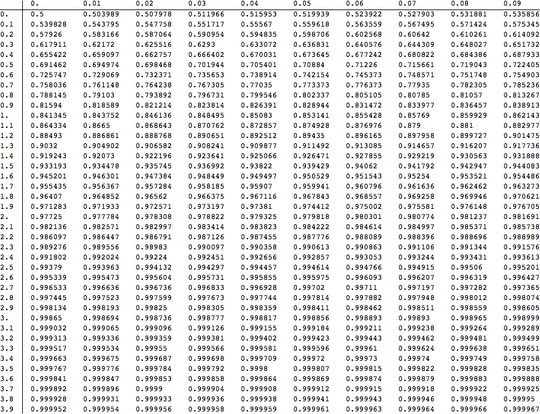
The canonical format for such a table appears to be:

    0.00    0.01    0.02    0.03    0.04    0.05    0.06    0.07    0.08    0.09
0.0 0.5000  0.5040  0.5080  0.5120  0.5160  0.5199  0.5239  0.5279  0.5319  0.5359
0.1 0.5398  0.5438  0.5478  0.5517  0.5557  0.5596  0.5636  0.5675  0.5714  0.5753
0.2 0.5793  0.5832  0.5871  0.5910  0.5948  0.5987  0.6026  0.6064  0.6103  0.6141
0.3 0.6179  0.6217  0.6255  0.6293  0.6331  0.6368  0.6406  0.6443  0.6480  0.6517
0.4 0.6554  0.6591  0.6628  0.6664  0.6700  0.6736  0.6772  0.6808  0.6844  0.6879
0.5 0.6915  0.6950  0.6985  0.7019  0.7054  0.7088  0.7123  0.7157  0.7190  0.7224
0.6 0.7257  0.7291  0.7324  0.7357  0.7389  0.7422  0.7454  0.7486  0.7517  0.7549
0.7 0.7580  0.7611  0.7642  0.7673  0.7704  0.7734  0.7764  0.7794  0.7823  0.7852
0.8 0.7881  0.7910  0.7939  0.7967  0.7995  0.8023  0.8051  0.8078  0.8106  0.8133
0.9 0.8159  0.8186  0.8212  0.8238  0.8264  0.8289  0.8315  0.8340  0.8365  0.8389
1.0 0.8413  0.8438  0.8461  0.8485  0.8508  0.8531  0.8554  0.8577  0.8599  0.8621
1.1 0.8643  0.8665  0.8686  0.8708  0.8729  0.8749  0.8770  0.8790  0.8810  0.8830
1.2 0.8849  0.8869  0.8888  0.8907  0.8925  0.8944  0.8962  0.8980  0.8997  0.9015
1.3 0.9032  0.9049  0.9066  0.9082  0.9099  0.9115  0.9131  0.9147  0.9162  0.9177
1.4 0.9192  0.9207  0.9222  0.9236  0.9251  0.9265  0.9279  0.9292  0.9306  0.9319
1.5 0.9332  0.9345  0.9357  0.9370  0.9382  0.9394  0.9406  0.9418  0.9429  0.9441
1.6 0.9452  0.9463  0.9474  0.9484  0.9495  0.9505  0.9515  0.9525  0.9535  0.9545
1.7 0.9554  0.9564  0.9573  0.9582  0.9591  0.9599  0.9608  0.9616  0.9625  0.9633
1.8 0.9641  0.9649  0.9656  0.9664  0.9671  0.9678  0.9686  0.9693  0.9699  0.9706
1.9 0.9713  0.9719  0.9726  0.9732  0.9738  0.9744  0.9750  0.9756  0.9761  0.9767
2.0 0.9772  0.9778  0.9783  0.9788  0.9793  0.9798  0.9803  0.9808  0.9812  0.9817
2.1 0.9821  0.9826  0.9830  0.9834  0.9838  0.9842  0.9846  0.9850  0.9854  0.9857
2.2 0.9861  0.9864  0.9868  0.9871  0.9875  0.9878  0.9881  0.9884  0.9887  0.9890
2.3 0.9893  0.9896  0.9898  0.9901  0.9904  0.9906  0.9909  0.9911  0.9913  0.9916
2.4 0.9918  0.9920  0.9922  0.9925  0.9927  0.9929  0.9931  0.9932  0.9934  0.9936
2.5 0.9938  0.9940  0.9941  0.9943  0.9945  0.9946  0.9948  0.9949  0.9951  0.9952
2.6 0.9953  0.9955  0.9956  0.9957  0.9959  0.9960  0.9961  0.9962  0.9963  0.9964
2.7 0.9965  0.9966  0.9967  0.9968  0.9969  0.9970  0.9971  0.9972  0.9973  0.9974
2.8 0.9974  0.9975  0.9976  0.9977  0.9977  0.9978  0.9979  0.9979  0.9980  0.9981
2.9 0.9981  0.9982  0.9982  0.9983  0.9984  0.9984  0.9985  0.9985  0.9986  0.9986
3.0 0.9987  0.9987  0.9987  0.9988  0.9988  0.9989  0.9989  0.9989  0.9990  0.9990
3.1 0.9990  0.9991  0.9991  0.9991  0.9992  0.9992  0.9992  0.9992  0.9993  0.9993
3.2 0.9993  0.9993  0.9994  0.9994  0.9994  0.9994  0.9994  0.9995  0.9995  0.9995
3.3 0.9995  0.9995  0.9995  0.9996  0.9996  0.9996  0.9996  0.9996  0.9996  0.9997
3.4 0.9997  0.9997  0.9997  0.9997  0.9997  0.9997  0.9997  0.9997  0.9997  0.9998
3.5 0.9998  0.9998  0.9998  0.9998  0.9998  0.9998  0.9998  0.9998  0.9998  0.9998
3.6 0.9998  0.9998  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999
3.7 0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999
3.8 0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999  0.9999
3.9 1.0000  1.0000  1.0000  1.0000  1.0000  1.0000  1.0000  1.0000  1.0000  1.0000

student

Posted 2012-11-24T12:29:04.117

Reputation: 71

do you want to exclude the inevitable boring answers in languages which have a built-in function to do this? – Peter Taylor – 2012-11-24T13:37:36.127

Yes. No build-in functions. – student – 2012-11-24T13:38:54.040

1Also, do you want to place a limit on running time or are you willing to accept Monte-Carlo approaches (probably based on Box-Müller)? – Peter Taylor – 2012-11-24T13:39:43.410

I haven't thought that but it would be nice that the program will halt in reasonable time. But it is hard to say what would be reasonable. – student – 2012-11-24T13:42:38.663

@PeterTaylor Nice idea. As far as run time, MC solutions would only need to run on order of 10^9 total throws to achieve the expected precision. Maybe 10^11 to be confident. On a multi-GHz, superscaler machine that halts in a few minutes. Maybe better if you are able to take advantage of of the SIMD unit (thought is is not clear that you can). – dmckee --- ex-moderator kitten – 2012-11-24T17:28:38.140

Is the cannonical format requried, or anything that contains the correct values? – ugoren – 2012-11-25T05:45:15.263

@dmckee, you're not likely to take advantage of the SIMD unit in golf anyway. And on reflection, Monte-Carlo is probably going to require more code than basic direct quadrature. – Peter Taylor – 2012-11-25T15:19:43.093

Answers

3

Mathematica 132 136 127

If Erfc is acceptable, here's my attempt, accurate to 6 places:

t=Table;TableForm[Partition[t[0.5 Erfc[-x/Sqrt[2]],{x,0,3.99,.01}],10], 
TableHeadings->{t[k,{k,0,3.9,.1}],t[k,{k,0,.09,.01}]}]

enter image description here

DavidC

Posted 2012-11-24T12:29:04.117

Reputation: 24 524

Someone needs to tell Wolfram what a significant figure is. 0.5 isn't the same as 0.500000. – Peter Taylor – 2012-11-25T15:21:27.107

Interesting point. If one uses ScientificForm[number,4], the output will display, at most, four digits (times a power of 10), but it still truncates zeros to the right. So ScientificForm[0.5 ,3] returns 5. * 10^(-1). EngineeringForm[.5,3] shows similar inconsistencies. – DavidC – 2012-11-25T16:25:40.730

(I know this answer is old but) If you want to be explicit about the precision, use 0.5`1 or 0.5`6. 0.5 and 0.500000 both have machine precision. – user202729 – 2018-11-19T05:15:05.790

2

GolfScript (124 chars)

10:&,~]'    0.0'*40,{n\:I&/'.'I&%&,{'   '\I&*+&8?:^*100/:x^54,-2%{:i*x.{*^/}:$~$i).)*/^\-}/$3989423$15000500+`5<(49-'.'@}%}/

Note: the only whitespace in there are two tab characters. MarkDown is turning them into triple-spaces.

The interesting part (i.e. the calculation) is done in x.8 fixpoint using identity 26.2.10 of Abramowitz and Stegun (1972). The program runs in under 2 seconds on my machine.

Peter Taylor

Posted 2012-11-24T12:29:04.117

Reputation: 41 901

1

k

This is based on the Zelen and Severo algorithm here. 162 characters. Can improve the character count significantly by reducing precision.

+`q`p!(q;{abs(x>0)-(exp[-.5*x*x]%sqrt 2*acos -1)*t*.31938153+t*-.356563782+t*1.781477937+t*-1.821255978+1.330274429*t:1%1+.2316419*abs x}(q:0.1*!391)+\:0.01*!100)

Runs in about 15ms on a Pentium E2160.

skeevey

Posted 2012-11-24T12:29:04.117

Reputation: 4 139

1

Perl - 137 133 bytes

print"\t0.0$_"for 0..9;for($f=2.506628;$i++<80;$f*=-++$i){printf'
%.1f',$x,s;;+\$x**$i/$i/$f;;printf"\t%.4f",eval,$x+=.01for(.5.$_)x10}

(both \t should be replaced with a literal tab character.)

Uses a Taylor Series expansion[1], adding one term per row, which seems to be good enough. The script produces the output exactly as expected, although each row does have a trailing whitespace. Runs in about 60ms on my lappy.

Edit as per comment by Peter Taylor.

[1] http://mathworld.wolfram.com/NormalDistributionFunction.html (formula 10)

primo

Posted 2012-11-24T12:29:04.117

Reputation: 30 891

Hmm - MarkDown probably clobbered the tabs that were in the table when I pasted it. If you replace the spaces in the first format string by a single tab character and change the last format string into <TAB>%.4f then you get the correct output and save 4 chars. – Peter Taylor – 2012-11-24T17:15:16.440

1

c -- 372

Just for interest this is an implementation of Peter's Monte Carlo suggestion from the comments

#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#define P printf
#define F(c,n) for(c=0;c<n;++c)
long c=9e9,i,j,k;double a[400],b=.01,t;
double B(){return sqrt(-2*log(drand48()))*cos(2*M_PI*drand48());}main()
{srand48(time(0));F(i,c){t=B();F(k,400)a[k] += t<b*k;}P("%4c",' ');F(j,10)
P("%4.2f    ",b*j);F(i,40){P("\n%3.1f ",10*i*b);F(j,10)
P("%6.4f  ",a[10*i+j]/c);}}

Lots of repetitive code. A very straight forward implementation, ungolfed it looks like 

#include "stdio.h"
#include "stdlib.h"
#include "math.h"

long c=9e9, i, j, k;  /* demands longs longer than 32 bits */

double a[400], bw=.01, t;

double B/*oxMuller*/(){
 /* normal distribution, centered on 0, std dev 1 */
  return sqrt(-2*log(drand48())) * cos(2*M_PI*drand48());
}

main(){
  srand48(time(0));
  for(i=0; i<c; ++i) { /* compute the probabilities by MC integration */
    t=B/*oxMuller*/();
    for(k=0; k<400; ++k) a[k] += t<bw*k;
  }
  /* Print the table */
  printf("%4c",' ');
  for(j=0; j<10; ++j) printf("%4.2f    ",bw*j);
  for(i=0; i<40; ++i) {
    printf("\n%3.1f ",10*i*bw);
    for(j=0; j<10; ++j) printf("%6.4f  ",a[10*i+j]/c);
  }
  printf("\n"); /* make the end pretty */
}

It is slow, about 60 seconds to do 100,000,000 throws with absolutely all the optimization bells and whistles turned on (-m64 -Ofast) on my 2.2 GHz Core 2 Duo laptop. Worse, it needs circa 50 times that many to provide real confidence that you have the right value in each and every bin. As written I'm asking for even more.

That seems too long to me, but I suspect that I underestimate how much work drand48 is doing (and I have sacrificed about a factor of 2 in the random number generation at the alter of small code).

It also demands that long is a bit bigger than 32 bits (thus the -m64 above).

dmckee --- ex-moderator kitten

Posted 2012-11-24T12:29:04.117

Reputation: 2 726

drand48() is not the problem; you're being hit by branch misprediction. I got a >3X performance improvement when I replaced for(k=0; k<400; ++k) a[k] += t<bw*k; with for( k=t<0?0:ceil(t/bw); k<400; ++k) a[k]+=1; – ceilingcat – 2018-04-03T04:28:52.647

Asked: 2012-11-24T12:29:04.117

Viewed: 3 253 times

Active: 2013-06-26T13:37:19.307