30
1
The Stern-Brocot sequence is a Fibonnaci-like sequence which can be constructed as follows:
- Initialise the sequence with
s(1) = s(2) = 1 - Set counter
n = 1 - Append
s(n) + s(n+1)to the sequence - Append
s(n+1)to the sequence - Increment
n, return to step 3
This is equivalent to:
Amongst other properties, the Stern-Brocot sequence can be used to generate every possible positive rational number. Every rational number will be generated exactly once, and it will always appear in its simplest terms; for example, 1/3 is the 4th rational number in the sequence, but the equivalent numbers 2/6, 3/9 etc won't appear at all.
We can define the nth rational number as r(n) = s(n) / s(n+1), where s(n) is the nth Stern-Brocot number, as described above.
Your challenge is to write a program or function which will output the nth rational number generated using the Stern-Brocot sequence.
- The algorithms described above are 1-indexed; if your entry is 0-indexed, please state in your answer
- The algorithms described are for illustrative purposes only, the output can be derived in any way you like (other than hard-coding)
- Input can be via STDIN, function parameters, or any other reasonable input mechanism
- Ouptut can be to STDOUT, console, function return value, or any other reasonable output stream
- Output must be as a string in the form
a/b, whereaandbare the relevant entries in the Stern-Brocot sequence. Evaluating the fraction before output is not permissable. For example, for input12, output should be2/5, not0.4. - Standard loopholes are disallowed
This is code-golf, so shortest answer in bytes will win.
Test cases
The test cases here are 1-indexed.
n r(n)
-- ------
1 1/1
2 1/2
3 2/1
4 1/3
5 3/2
6 2/3
7 3/1
8 1/4
9 4/3
10 3/5
11 5/2
12 2/5
13 5/3
14 3/4
15 4/1
16 1/5
17 5/4
18 4/7
19 7/3
20 3/8
50 7/12
100 7/19
1000 11/39
OEIS entry: A002487
Excellent Numberphile video discussing the sequence: Infinite Fractions
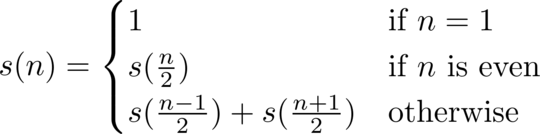
Can the output use
Trues instead of1s? – Loovjo – 2016-08-18T13:54:19.9601@Loovjo No,
True/2isn't a valid fraction (as far as I'm concerned). As an aside,Trueisn't always1- some languages use-1instead to avoid potential mistakes when applying bitwise operators. [citation needed] – Sok – 2016-08-18T14:01:48.257related – flawr – 2016-08-18T15:40:45.523
2
@Sok citation
– mbomb007 – 2016-08-18T17:13:13.3731@Sok but in Python,
Trueis equivalent to1andTrue/2would be1/2. – Leaky Nun – 2016-08-20T08:06:06.263Are equivalent representations (like
-2/-1 == 2/1or4/2 == 2/1) acceptable? – Mego – 2016-08-20T08:46:12.743@LeakyNun That may be the case, but
Trueis not the same in every language. This would open the door to different representations coming from different languages. In my opinion, the output from every language should be consistent, so I'm not allowingTruein the place of1– Sok – 2016-08-20T09:33:38.303@Mego No, as the fractions should be generated using some variation of the Stern-Brocot sequence. Negative numbers don't feature in that sequence, and as noted in the question, every rational number generated will be in its simplest terms. – Sok – 2016-08-20T09:35:17.740