Number Plate Golf: Recognition

Question

See also: Parsing

Introduction

You're working on a government programming team, who have been programming the speed cameras. However, the group of people who have programmed the speed calculator have taken up too much space, so you have to make the number plate recognition software as small as possible.

Challenge

Given an image of a number plate, return the text on the plate.

Number plates

The following are all of the characters which your program must recognise:

ABCDEFG

H1JKLMN0

PQRSTUVW

XYZ01234

56789

Note

On British number plates, the characters for I (i) and 1 (one) are the same and the characters for O (o) and 0 (zero) are the same. For that reason, always assume characters are the numbers. I.e. the following number plate is 10 (one zero):

Examples

C0D3 GLF

B3T4 DCY

M1NUS 15

YET1CGN

Other rules

Internet access and OCR libraries and functions are disallowed.

The number plates will always look identical to the ones shown above. All number plates will be roughly same size (there will be some inaccuracies due to cropping method).

If you require lossless PNG versions of any number plates, I will supply them to you.

Scoring

The shortest program in bytes wins.

_{All number plates are screenshots of the search bar at this site}

Answer 1

C, 409 bytes (and I'm as surprised as anybody)

f(w,h,d,X,T,B,x,y,b,v,u,t,a)char*d;{for(x=X=0;++x<w;){for(y=b=h;y--;a=0)d[(y*w+x)*3+1]&224||(b=0,X||(X=x,T=B=y),T=y<T?y:T,B=y>B?y:B);if(X*b){for(B+=1-T,X=x-X,v=5;v--;)for(u=4;u--;a|=(b>X/4*(B/5)*.35)<<19-u*5-v)for(b=0,t=X/4;t--;)for(y=B/5;y--;)b+=!(d[((v*B/5+y+T)*w+x-X+u*X/4+t)*3+1]&224);X=!putchar("g------a----mj---et-u--6----7--8s4-c-x--q--d9xy5-0v--n-2-hw-k-----3---bf-----t-r---pzn-1---l"[a%101-7]);}}}

Takes as input: the width (w) and height (h) of the image, followed by the packed RGB data as an array of chars (d). All the other function parameters are variable declarations in disguise. Ignores everything except the green channel, and applies a threshold of 32 as an initial pass.

Mostly the same as @DavidC's method, except this checks that at least 35% of each sample box is filled. Hopefully that makes it more robust to scale changes, but who knows.

I used a brute-force method to find out which resampling size and coverage percent to use for the best reliability (i.e. fewest cases of one character having multiple interpretations). It turned out that a 4x5 grid with 35% coverage was best. I then used a second brute-force method to calculate the best bit arrangement and modulo value to pack the character data into a short string — the low bit at the top-left, increasing in x then y, with the final value % 101 turned out best, giving this lookup table:

-------g------a----mj---et-u--6----7--8s4-c-x--q--d9xy5-0v--n-2-hw-k-----3---bf-----t-r---pzn-1---l--

Subtracting 7 means the initial -'s can be removed, and the last 2 can be removed without any extra work. This removal means that certain invalid inputs could cause an invalid memory read, so it could segfault on particular images.

Usage:

To get the images into it, I wrote a wrapper using libpng. Also it turns out that despite the filename, the images in the question are actually jpegs (!), so you'll need to manually export them as pngs first.

#include <png.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main(int argc, const char *const *argv) {
    if(argc < 2) {
        fprintf(stderr, "Usage: %s <file.png>\n", argv[0]);
        return 1;
    }

    const char *file = argv[1];

    FILE *const fp = fopen(file, "rb");
    if(fp == NULL) {
        fprintf(stderr, "Failed to open %s for reading\n", file);
        return 1;
    }

    png_structp png_ptr = png_create_read_struct(
        PNG_LIBPNG_VER_STRING, NULL, NULL, NULL
    );

    if(!png_ptr) {
        fclose(fp);
        fprintf(stderr, "Failed to initialise LibPNG (A)\n");
        return 1;
    }

    png_infop info_ptr = png_create_info_struct(png_ptr);

    if(!info_ptr) {
        png_destroy_read_struct(&png_ptr, NULL, NULL);
        fclose(fp);
        fprintf(stderr, "Failed to initialise LibPNG (B)\n");
        return 1;
    }

    if(setjmp(png_jmpbuf(png_ptr))) {
        png_destroy_read_struct(&png_ptr, &info_ptr, NULL);
        fclose(fp);
        fprintf(stderr, "Error while reading PNG\n");
        return 1;
    }

    png_init_io(png_ptr, fp);
    png_set_sig_bytes(png_ptr, 0);

    png_read_png(
        png_ptr, info_ptr,
        PNG_TRANSFORM_STRIP_16 |
        PNG_TRANSFORM_GRAY_TO_RGB |
        PNG_TRANSFORM_STRIP_ALPHA,
        NULL
    );
    const png_bytep *const rows = png_get_rows(png_ptr, info_ptr);
    const int w = png_get_image_width(png_ptr, info_ptr);
    const int h = png_get_image_height(png_ptr, info_ptr);
    unsigned char *const data = malloc(w*h*3 * sizeof(unsigned char));
    for(int y = 0; y < h; ++ y) {
        for(int x = 0; x < w; ++ x) {
            memcpy(&data[y*w*3], rows[y], w * 3 * sizeof(unsigned char));
        }
    }
    png_destroy_read_struct(&png_ptr, &info_ptr, NULL);
    fclose(fp);

    f(w, h, (char*) data);

    free(data);

    return 0;
}

Breakdown

f(                          // Function
    w,h,d,                  // Parameters: width, height, RGB data
    X,T,B,x,y,b,v,u,t,a     // Variables
)char*d;{                   // K&R syntax to save lots of type decls
  for(x=X=0;++x<w;){        // Loop through each column of the image:
    for(y=b=h;y--;a=0)      //  Loop through pixels in column:
      d[(y*w+x)*3+1]&224||( //   If green < 32: (char could be signed or unsigned)
        b=0,                //    This is not a blank line
        X||(X=x,T=B=y),     //    Start a new character if not already in one
        T=y<T?y:T,          //    Record top of character
        B=y>B?y:B           //    Record bottom of character
      );
    if(X*b){                //  If we just found the end of a character:
      // Check cell grid & record bits into "a"
      for(B+=1-T,X=x-X,v=5;v--;)
        for(u=4;u--;a|=(b>X/4*(B/5)*.35)<<19-u*5-v)
          // Calculate coverage of current cell
          for(b=0,t=X/4;t--;)
            for(y=B/5;y--;)
              b+=!(d[((v*B/5+y+T)*w+x-X+u*X/4+t)*3+1]&224);

      // Look up meaning of "a" in table & print, reset X to 0
      X=!putchar(
        "g------a----mj---et-u--6----7--8s4-c-x--q--d9x"
        "y5-0v--n-2-hw-k-----3---bf-----t-r---pzn-1---l"
        [a%101-7]
      );
    }
  }
}

Answer 2

Mathematica 1170 1270 1096 1059 650 528 570 551 525 498 bytes

The latest version saves 27 bytes by not requiring that the plate be "trimmed" before it is parsed. The penultimate version saved 26 bytes by using only 10 of the original 24 sample points.

z=Partition;h@i_:=i~PixelValue~#/.{_,_,_,z_}:>⌈z⌉&/@z[{45,99,27,81,63,81,9,63,45,63,9,45,45,45,63,45,45,27,45,9},2];f@p_:=h/@SortBy[Select[p~ColorReplace~Yellow~ComponentMeasurements~{"Image","Centroid"},100<Last@ImageDimensions@#[[2,1]]<120&],#[[2,2,1]]&][[All,2,1]]/.Thread[IntegerDigits[#,2,10]&/@(z[IntegerDigits[Subscript["ekqeuiv5pa5rsebjlic4i5886qsmvy34z5vu4e7nlg9qqe3g0p8hcioom6qrrkzv4k7c9fdc3shsm1cij7jrluo", "36"]],4]/.{a__Integer}:> FromDigits[{a}])-> Characters@"BD54TARP89Q0723Z6EFGCSWMNVYXHUJKL1"]

---

122 bytes saved through LegionMammal978's idea of packing the long list of base 10 numbers as a single, base 36 number. He pared another 20 bytes off the final code.

The jump from 528 to 570 bytes was due to additional code to ensure that the order of the letters returned corresponded to the order of the letters on the license plate. The centroid for each letter contains the x-coordinate, which reveals the relative positions of the letters along x.

---

Ungolfed Code

coordinates=Flatten[Table[{x,y},{y,99,0,-18},{x,9,72,18}],1];
h[img_] :=ArrayReshape[PixelValue[img, #] /. {_, _, _, z_} :>  ⌈z⌉  & /@ coordinates, {6, 4}];
plateCrop[img_]:=ColorReplace[ImageTrim[img,{{100,53},{830,160}}],Yellow];
codes={{{15,13,15,13,13,15},"B"},{{15,8,8,8,9,15},"C"},{{15,13,13,13,13,15},"D"},{{15,8,14,8,8,15},"E"},{{15,8,14,8,8,8},"F"},{{15,8,8,11,9,15},"G"},{{6,6,6,6,15,9},"A"},{{9,9,15,15,9,9},"H"},{{8,8,8,8,8,15},"L"},{{9,15,15,15,13,9},"M"},{{15,9,9,9,9,15},"0"},{{9,10,12,14,10,9},"K"},{{9,13,13,11,11,9},"N"},{{8,8,8,8,8,8},"1"},{{1,1,1,1,9,15},"J"},{{15,9,15,14,8,8},"P"},{{15,9,9,9,15,15},"Q"},{{15,9,15,14,10,11},"R"},{{15,8,12,3,1,15},"S"},{{9,15,6,6,6,6},"V"},{{15,6,6,6,6,6},"T"},{{9,15,15,15,15,15},"W"},{{9,9,9,9,9,15},"U"},{{9,14,6,6,14,9},"X"},{{9,14,6,6,6,6},"Y"},{{15,3,2,4,12,15},"Z"},{{15,9,9,9,9,15},"0"},{{8,8,8,8,8,8},"1"},{{15,1,3,6,12,15},"2"},{{15,1,3,1,9,15},"3"},{{2,6,6,15,2,2},"4"},{{7,12,14,1,1,15},"5"},{{15,8,14,9,9,15},"6"},{{15,1,2,2,6,4},"7"},{{15,9,15,9,9,15},"8"},{{15,9,15,1,9,15},"9"}};
decryptRules=Rule@@@codes;
isolateLetters[img_]:=SortBy[Select[ComponentMeasurements[plateCrop[img],{"Image","Centroid"}],ImageDimensions[#[[2,1]]][[2]]>100&],#[[2,2,1]]&][[All,2,1]]
f[plate_]:=FromDigits[#,2]&/@#&/@h/@isolateLetters[plate]/.decryptRules

Overview

The basic idea is to check whether a systematic sampling of pixels from the input image matches pixels from the same location on the bonafide images. Much of the code consists of the bit signatures for each character,

The diagram shows the pixels that are sampled from the letters "J", "P","Q", and "R".

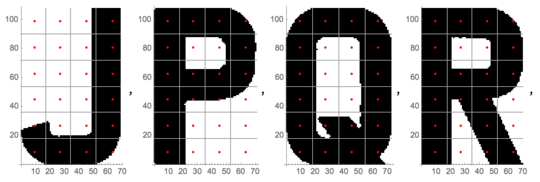
The pixel values can be represented as matrices. The dark, bold 1's correspond to black cells. The 0's correspond to white cells.

These are the decryption replacement rules for J P Q R.

{1, 1, 1, 1, 9, 15} -> "J",
{15, 9, 15, 14, 8, 8} -> "P",
{15, 9, 9, 9, 15, 15} -> "Q",
{15, 9, 15, 14, 10, 11} -> "R"

It should be possible to understand why the rule for "0" is:

{15, 9, 9, 9, 9, 15} -> "0"

and thus distinguishable from the letter "Q".

---

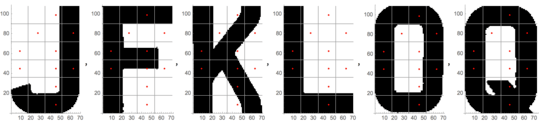
The following shows the 10 points used in the final version. These points are sufficient for identifying all of the characters.

---

What the functions do

plateCrop[img] removes the frame and left edge from the plate, makes the background white. I was able to eliminate this function from the final version by selecting image components, possible letters that were between 100 and 120 pixels high.

---

isolateLetters[img] removes the individual letters from the cropped image.

We can display how it works by showing where the cropped image, output from plateCrop goes as input for isolateLetters. The output is a list of individual characters.

---

Coordinates are 24 evenly distributed positions for checking the pixel color. The coordinates correspond to those in the first figure.

coordinates=Flatten[Table[{x,y},{y,99,0,-18},{x,9,72,18}],1];

{{9, 99}, {27, 99}, {45, 99}, {63, 99}, {9, 81}, {27, 81}, {45, 81}, {63, 81}, {9, 63}, {27, 63}, {45, 63}, {63, 63}, {9, 45}, {27, 45}, {45, 45}, {63, 45}, {9, 27}, {27, 27}, {45, 27}, {63, 27}, {9, 9}, {27, 9}, {45, 9}, {63, 9}}

---

h converts the pixels to binary.

h[img_] :=ArrayReshape[PixelValue[img, #] /. {_, _, _, z_} :>  ⌈z⌉  & /@ coordinates, {6, 4}];

---

codes are the signature for each character. The decimal values are abbreviations of the binary code for black (0) and White (1) cells. In the golfed version, base 36 is used.

codes={{{15, 9, 9, 9, 9, 15}, "0"}, {{8, 8, 8, 8, 8, 8}, "1"}, {{15, 1, 3,6,12, 15}, "2"}, {{15, 1, 3, 1, 9, 15}, "3"}, {{2, 6, 6, 15, 2, 2}, "4"}, {{7, 12, 14, 1, 1, 15},"5"}, {{15, 8, 14, 9, 9, 15}, "6"}, {{15, 1, 2, 2, 6, 4},"7"}, {{15, 9, 15, 9, 9, 15}, "8"}, {{15, 9, 15, 1, 9, 15},"9"}, {{6, 6, 6, 6, 15, 9}, "A"}, {{15, 13, 15, 13, 13, 15}, "B"}, {{15, 8, 8, 8, 9, 15}, "C"}, {{15, 13, 13, 13, 13, 15}, "D"}, {{15, 8, 14, 8, 8, 15}, "E"}, {{15, 8, 14, 8, 8, 8},"F"}, {{15, 8, 8, 11, 9, 15}, "G"}, {{9, 9, 15, 15, 9, 9}, "H"}, {{1, 1, 1, 1, 9, 15}, "J"}, {{9, 10, 12, 14, 10, 9}, "K"}, {{8, 8, 8, 8, 8, 15}, "L"}, {{9, 15, 15, 15, 13, 9}, "M"}, {{9, 13, 13, 11, 11, 9}, "N"}, {{15, 9, 15, 14, 8, 8}, "P"}, {{15, 9, 9, 9, 15, 15}, "Q"}, {{15, 9, 15, 14, 10, 11}, "R"}, {{15, 8, 12, 3, 1, 15}, "S"}, {{15, 6, 6, 6, 6, 6}, "T"}, {{9, 9, 9, 9, 9, 15}, "U"}, {{9, 15, 6, 6, 6, 6}, "V"}, {{9, 15, 15, 15, 15, 15}, "W"}, {{9, 14, 6, 6, 14, 9}, "X"}, {{9, 14, 6, 6, 6, 6}, "Y"}, {{15, 3, 2, 4, 12, 15}, "Z"}};

(* decryptRules are for replacing signatures with their respective character *)

decryptRules=Rule@@@codes;

f is the function that takes an image of a license plate and returns a letter.

f[plate_]:=FromDigits[#,2]&/@#&/@h/@isolate[plateCrop@plate]/.decryptRules;

{"A", "B", "C", "D", "E", "F", "G"}
{"H", "1", "J", "K", "L", "M", "N", "0"}
{"P", "Q", "R", "S", "T", "U", "V", "W"}
{"X", "Y", "Z", "0", "1", "2", "3", "4"}
{"5", "6", "7", "8", "9"}

---

Golfed

The code is shortened by using a single decimal number to represent all 24 bits (white or black) for each character. For example, the letter "J" uses the following replacement rule: 1118623 -> "J".

1118623 corresponds to

IntegerDigits[1118623 , 2, 24]

{0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1}

which can be repackaged as

ArrayReshape[{0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1}, {6, 4}]

{{0, 0, 0, 1}, {0, 0, 0, 1}, {0, 0, 0, 1}, {0, 0, 0, 1}, {1, 0, 0, 1}, {1, 1, 1, 1}}

which is simply the matrix for "J" that we saw above.

%//MatrixForm

Another savings comes from representing the alphabet as "0123456789ABCDEFGHJKLMNPQRSTUVWXYZ" rather than as a list of letters.

Finally, all of the functions from the long version, except h, were integrated into the function f rather than defined separately.

---

h@i_:=ArrayReshape[i~PixelValue~#/.{_,_,_,z_}:>⌈z⌉&/@Join@@Table[{x,y},{y,99,0,-18},{x,9,72,18}],{6,4}];f@p_:=#~FromDigits~2&/@(Join@@@h/@SortBy[Select[p~ImageTrim~{{100,53},{830,160}}~ColorReplace~Yellow~ComponentMeasurements~{"Image","Centroid"},Last@ImageDimensions@#[[2,1]]>100&],#[[2,2,1]]&][[;;,2,1]])/.Thread[IntegerDigits[36^^1c01agxiuxom9ds3c3cskcp0esglxf68g235g1d27jethy2e1lbttwk1xj6yf590oin0ny1r45wc1i6yu68zxnm2jnb8vkkjc5yu06t05l0xnqhw9oi2lwvzd5f6lsvsb4izs1kse3xvx694zwxz007pnj8f6n,8^8]->Characters@"J4A51LUHKNYXVMW732ZTCGSFE60Q98PRDB"]

Answer 3

C#, 1040 1027 bytes

using System;using System.Drawing;class _{static Bitmap i;static bool b(int x,int y)=>i.GetPixel(x,y).GetBrightness()<.4;static char l(int x,int y){if(y<45)return b(x+5,145)?((b(x+30,100)||b(x+30,50))?(b(x+68,94)?(b(x+40,50)?'D':b(x+40,120)?(b(x+45,80)?'M':'N'):'H'):b(x,97)?(b(x+30,140)?'E':b(x+60,70)?(b(x+50,140)?'R':'P'):'F'):b(x+65,45)?(b(x+5,100)?'K':b(x+30,145)?'Z':'X'):'B'):b(x+30,140)?'L':'1'):b(x+30,55)?(b(x+60,70)?'7':'T'):b(x+2,100)?'U':b(x+30,70)?'W':b(x+15,100)?'V':'Y';if(y<70)return b(x+50,110)?(b(x+50,70)?(b(x+10,110)?(b(x+30,100)?(b(x+55,80)?'8':'6'):b(x+55,80)?'0':'G'):b(x+10,70)?(b(x+60,80)?'9':'S'):b(x+60,120)?'3':'2'):'G'):b(x+30,125)?'Q':'C';if(y>150)return'A';if(y>120)return'J';else return b(x+10,135)?'5':'4';}static void Main(string[]z){i=new Bitmap(Console.ReadLine());bool s=true;int w=int.MinValue;for(int x=100;x<800;++x){for(int y=40;y<160;++y)if(s){if(b(x,y)){if(w>50)Console.Write(' ');Console.Write(l(x,y));s=false;goto e;}}else if(b(x,y))goto e;if(!s){s=true;w=0;}else++w;e:continue;}}}

Ungolfed:

using System;
using System.Drawing;

class _
{
    static Bitmap bmp;
    static bool b(int x, int y) => bmp.GetPixel(x, y).GetBrightness() < .4;
    static char l(int x, int y)
    {
        if (y < 45)
            return b(x + 5, 145) ? ((b(x + 30, 100) || b(x + 30, 50)) ? (b(x + 68, 94) ? (b(x + 40, 50) ? 'D' : b(x + 40, 120) ? (b(x + 45, 80) ? 'M' : 'N') : 'H') : b(x, 97) ? (b(x + 30, 140) ? 'E' : b(x + 60, 70) ? (b(x + 50, 140) ? 'R' : 'P') : 'F') : b(x + 65, 45) ? (b(x + 5, 100) ? 'K' : b(x + 30, 145) ? 'Z' : 'X') : 'B') : b(x + 30, 140) ? 'L' : '1') : b(x + 30, 55) ? (b(x + 60, 70) ? '7' : 'T') : b(x + 2, 100) ? 'U' : b(x + 30, 70) ? 'W' : b(x + 15, 100) ? 'V' : 'Y';
        if (y < 70)
            return b(x + 50, 110) ? (b(x + 50, 70) ? (b(x + 10, 110) ? (b(x + 30, 100) ? (b(x + 55, 80) ? '8' : '6') : b(x + 55, 80) ? '0' : 'G') : b(x + 10, 70) ? (b(x + 60, 80) ? '9' : 'S') : b(x + 60, 120) ? '3' : '2') : 'G') : b(x + 30, 125) ? 'Q' : 'C';
        if (y > 150)
            return 'A';
        if (y > 120)
            return 'J';
        if (y > 95)
            return b(x + 10, 135) ? '5' : '4';
        return '-';
    }
    static void Main(string[] args)
    {
        bmp = new Bitmap(Console.ReadLine());
        bool state = true;
        int space = int.MinValue;
        for (int x = 100; x < 800; ++x)
        {
            for (int y = 40; y < 160; ++y)
                if (state)
                {
                    if (b(x, y))
                    {
                        if (space > 50)
                            Console.Write(' ');
                        Console.Write(l(x, y));
                        state = false;
                        goto bad;
                    }
                }
                else if (b(x, y))
                    goto bad;
            if (!state)
            {
                state = true;
                space = 0;
            }
            else
                ++space;
            bad:
            continue;
        }
    }
}

Basically I found some specific reference points to check yellow/black to determine the identity of each character.

Answer 4

PHP – 1741 1674 1143 bytes

It was first set up by learning the profiles of the characters from the first few examples, which then summarized each character into six numbers. I chose six because I originally had five, and it didn't work as great as I'd like, but six seems to work much better. Much of the optimization involves squeezing these profiles into smaller and smaller byte counts.

The first and second profile *lhdfdn and |nnmmkk are actually the blue blob with "GB" at the bottom *, and the right border |, which we're ignoring. It's safer to include them so that the blob and right border have something to match against.

Should handle any image format, any reasonable scaling provided the aspect ratio doesn't change too much, any dark on light color, and even a bit of noise and shading!

It does need the border, at least at the top and bottom, that's part of the profile.

<?php $X=[];foreach(str_split('*lhdfdn|nnmmkkA<njjk;BOnKB`^Chn::E7DHn?1X`EnkGGD4Fn_330!Gnj9G[IHnX!!XnJ%(##knKnX.EN6LnX!!!!Mn_<:bnNn^77_nPn^33@6QhfBDjnRn_8LaDSOlYYnUT$$nn$$Uh_##^nV9c][n;W_nWTlhXHnLTiCY4LhnM5ZJbnmaI0ng88lk1nnnnnn2C[__n`34B?Kna4+=Fnb"5NnUReX6gnKKaM7*4Xnb=8gkIIne9K`KKni',7)as$s){$t=[];foreach(str_split(substr($s,1))as$u)$t[]=ord($u)-11;$X[$s[0]]=$t;}echo m(r($argv[1]),$X)."\n";function r($u){$a=[];$i=imagecreatefromstring(file_get_contents($u));$w=imagesx($i);$h=imagesy($i);$s=[];for($x=0;$x<$w;$x++){$s[$x]=0;for($y=0;$y<$h;$y++){$p=imagecolorsforindex($i,imagecolorat($i,$x,$y));if(3*$p['red']+6*$p['green']+$p['blue']<1280)$s[$x]++;}}$j=0;$k=[];for($x=0;$x<$w;$x++){if($s[$x]>$h/10)for($o=0;$o<6;$o++)$k[]=$s[$x];elseif(count($k)){$a[]=$k;$j++;$k=[];}}$b=[];foreach($a as$v){$t=[];$u=array_chunk($v,intval(count($v)/6));foreach($u as$c)$t[]=array_sum($c)/count($c);$m=99/max($t);$e=[];foreach($t as$x)$e[]=intval($x*$m+0.5);$b[]=$e;}return$b;}function m($A,$X){$r='';foreach($A as$a){$s=INF;$c='';foreach($X as$k=>$x){$t=0;for($i=0;$i<6;$i++)$t+=pow($a[$i]-$x[$i],2);if($s>$t){$s=$t;$c=$k;}}$r.=$c;}return trim($r,'|*');}

Save as ocr.php, then run from the command line:

$ php ocr.php http://i.imgur.com/UfI63md.png
ABCDEFG

$ php ocr.php http://i.imgur.com/oSAK7dy.png
H1JKLMN0

$ php ocr.php http://i.imgur.com/inuIHjm.png
PQRSTUVW

$ php ocr.php http://i.imgur.com/Th0QkhT.png
XYZ01234

$ php ocr.php http://i.imgur.com/igH3ZPQ.png
56789

$ php ocr.php http://i.imgur.com/YfVwebo.png
10

$ php ocr.php http://i.imgur.com/3ibQARb.png
C0D3GLF

$ php ocr.php http://i.imgur.com/c7XZqhL.png
B3T4DCY

$ php ocr.php http://i.imgur.com/ysBgXhn.png
M1NUS15

For those that are interested, here is the learning code. Save as learn.php and run from the command line, no arguments.

<?php

define('BANDS', 6);

main();

function main()
{
    $glyphs = [];

    learn($glyphs, 'http://imgur.com/UfI63md.png', '*ABCDEFG|');
    learn($glyphs, 'http://imgur.com/oSAK7dy.png', '*H1JKLMN0|');
    learn($glyphs, 'http://imgur.com/inuIHjm.png', '*PQRSTUVW|');
    learn($glyphs, 'http://imgur.com/Th0QkhT.png', '*XYZ01234|');
    learn($glyphs, 'http://imgur.com/igH3ZPQ.png', '*56789|');

    $profiles = summarize($glyphs);

    foreach ($profiles as $glyph=>$profile)
    {
        print $glyph;
        foreach ($profile as $value)
            print chr($value + 11);
        print "\n";
    }
}

function learn(&$glyphs, $url, $answer)
{
    $image = imagecreatefromstring(file_get_contents($url));
    $width = imagesx($image);
    $height = imagesy($image);
    $counts = [];
    for ($x = 0; $x < $width; $x++)
    {
        $counts[$x] = 0;
        for ($y = 0; $y < $height; $y++)
        {
            $pixel = imagecolorsforindex($image, imagecolorat($image, $x, $y));
            if (3 * $pixel['red'] + 6 * $pixel['green'] + $pixel['blue'] < 1280)
                $counts[$x]++;
        }
    }

    $index = 0;
    $expanded = [];
    for ($x = 0; $x < $width; $x++)
    {
        if ($counts[$x] > $height / 10)
            for ($inner = 0; $inner < BANDS; $inner++)
                $expanded[] = $counts[$x];
        else if (count($expanded)) {
            $glyphs[$answer[$index]] = $expanded;
            $index++;
            $expanded = [];
        }
    }
}

function summarize($glyphs)
{
    $profiles = [];
    foreach ($glyphs as $glyph=>$expanded)
    {
        $averages = [];
        $bands = array_chunk($expanded, count($expanded) / BANDS);
        foreach ($bands as $band)
            $averages[] = array_sum($band) / count($band);
        $scaling = 99 / max($averages);
        $profile = [];
        foreach ($averages as $average)
            $profile[] = intval($average * $scaling + 0.5);
        $profiles[$glyph] = $profile;
    }
    return $profiles;
}

?>

Answer 5

PHP, 971 970 bytes

Draws heavily upon Yimin Rong's answer, which can be seriously golfed down, especially the array indices, and put into a Phar with gzip compression.

Download the phar

This is my improved base version at 1557 1535 bytes, saved simply under the filename "o":

<?$X=[[99,92,45,45,97,96],[99,99,99,99,99,99],[56,80,84,84,99,85],[41,55,52,64,99,86],[32,50,59,99,87,23],[67,99,74,71,90,77],[92,99,64,64,86,66],[31,41,77,99,87,50],[92,96,62,62,99,90],[64,85,64,64,99,94],''=>[99,99,98,98,96,96],A=>[49,99,95,95,96,48],B=>[68,99,64,55,85,83],C=>[93,99,47,47,58,44],D=>[61,99,52,38,77,85],E=>[99,96,60,60,57,41],F=>[99,84,40,40,37,22],G=>[99,95,46,60,80,62],H=>[99,77,22,22,77,99],1=>[99,99,99,99,99,99],J=>[26,29,24,24,96,99],K=>[99,77,35,58,67,43],L=>[99,77,22,22,22,22],M=>[99,84,49,47,87,99],N=>[99,83,44,44,84,99],P=>[99,83,40,40,53,43],Q=>[93,91,55,57,95,99],R=>[99,84,45,65,86,57],S=>[68,97,78,78,99,74],T=>[25,25,99,99,25,25],U=>[93,84,24,24,83,99],V=>[46,88,82,80,99,48],W=>[84,99,76,73,97,93],X=>[61,99,65,73,94,56],Y=>[41,65,93,99,66,42],Z=>[63,87,99,98,86,62]];echo m(r($argv[1]),$X);function r($u){$a=[];$i=imagecreatefromstring(join('',file($u)));$w=imagesx($i);$h=imagesy($i);$s=[];for(;$x<$w;$x++){$s[$x]=0;for($y=0;$y<$h;$y++){$p=imagecolorsforindex($i,imagecolorat($i,$x,$y));if(3*$p[red]+6*$p[green]+$p[blue]<1280)$s[$x]++;}}$j=0;$k=[];for(;$z<$w;$z++){if($s[$z]>$h/10)for($o=0;$o<6;$o++)$k[]=$s[$z];elseif(count($k)){$a[]=$k;$j++;$k=[];}}$b=[];foreach($a as$v){$t=[];$u=array_chunk($v,~~(count($v)/6));foreach($u as$c)$t[]=array_sum($c)/count($c);$m=99/max($t);$e=[];foreach($t as$x)$e[]=~~($x*$m+.5);$b[]=$e;}return$b;}function m($A,$X){$r='';foreach($A as$a){$s=INF;$c='';foreach($X as$k=>$x){$t=0;for($i=0;$i<6;)$t+=($a[$i]-$x[$i++])**2;if($s>$t){$s=$t;$c=$k;}}$r.=$c;}return$r;}

Improvements:

1st stage

• Numeric array indices removed and reordered the array, string indices as implicit constants

2nd stage

• Replaced intval with ~~ (saves 8 bytes, two occurences)
• for-loop initialization removed where unnecessary
• file_get_contents($u) replaced with join('',file($u)) (saves 5 bytes)
• and a few others

Unfortunately, all the second stage improvements only translate into 1 byte less gzipped code. :-D

And this code was used to create the Phar:

<?php
$phar = new Phar('o.phar');
$phar->addFile('o');
$phar['o']->compress(Phar::GZ);
$phar->setStub('<?Phar::mapPhar(o.phar);include"phar://o.phar/o";__HALT_COMPILER();');

Test with php ocr.phar http://i.imgur.com/i8jkCJu.png or any other of the test case images.