Fastest semiprime factorization

Question

Write a program to factorize a semi-prime number in the shortest amount of time.

For testing purposes, use this: 38!+1 (523022617466601111760007224100074291200000001)

It is equal to: 14029308060317546154181 × 37280713718589679646221

Answer 1

Python (w/ PyPy JIT v1.9) ~1.9s

Using a Multiple Polynomial Quadratic Sieve. I took this to be a code challenge, so I opted not to use any external libraries (other than the standard log function, I suppose). When timing, the PyPy JIT should be used, as it results in timings 4-5 times faster than that of cPython.

Update (2013-07-29):
Since originally posting, I've made several minor, but significant changes which increase the overall speed by a factor of about 2.5x.

Update (2014-08-27):
As this post is still receiving attention, I've updated my_math.py correcting two errors, for anyone who may be using it:

• isqrt was faulty, sometimes producing incorrect output for values very close to a perfect square. This has been corrected, and the performance increased by using a much better seed.
• is_prime has been updated. My previous attempt to remove perfect square 2-sprps was half-hearted, at best. I've added a 3-sprp check - a technique used by Mathmatica - to ensure that the tested value is square-free.

Update (2014-11-24):
If at the end of the calculation no non-trivial congruencies are found, the progam now sieves additional polynomials. This was previously marked in the code as TODO.

---

mpqs.py

from my_math import *
from math import log
from time import clock
from argparse import ArgumentParser

# Multiple Polynomial Quadratic Sieve
def mpqs(n, verbose=False):
  if verbose:
    time1 = clock()

  root_n = isqrt(n)
  root_2n = isqrt(n+n)

  # formula chosen by experimentation
  # seems to be close to optimal for n < 10^50
  bound = int(5 * log(n, 10)**2)

  prime = []
  mod_root = []
  log_p = []
  num_prime = 0

  # find a number of small primes for which n is a quadratic residue
  p = 2
  while p < bound or num_prime < 3:

    # legendre (n|p) is only defined for odd p
    if p > 2:
      leg = legendre(n, p)
    else:
      leg = n & 1

    if leg == 1:
      prime += [p]
      mod_root += [int(mod_sqrt(n, p))]
      log_p += [log(p, 10)]
      num_prime += 1
    elif leg == 0:
      if verbose:
        print 'trial division found factors:'
        print p, 'x', n/p
      return p

    p = next_prime(p)

  # size of the sieve
  x_max = len(prime)*60

  # maximum value on the sieved range
  m_val = (x_max * root_2n) >> 1

  # fudging the threshold down a bit makes it easier to find powers of primes as factors
  # as well as partial-partial relationships, but it also makes the smoothness check slower.
  # there's a happy medium somewhere, depending on how efficient the smoothness check is
  thresh = log(m_val, 10) * 0.735

  # skip small primes. they contribute very little to the log sum
  # and add a lot of unnecessary entries to the table
  # instead, fudge the threshold down a bit, assuming ~1/4 of them pass
  min_prime = int(thresh*3)
  fudge = sum(log_p[i] for i,p in enumerate(prime) if p < min_prime)/4
  thresh -= fudge

  if verbose:
    print 'smoothness bound:', bound
    print 'sieve size:', x_max
    print 'log threshold:', thresh
    print 'skipping primes less than:', min_prime

  smooth = []
  used_prime = set()
  partial = {}
  num_smooth = 0
  num_used_prime = 0
  num_partial = 0
  num_poly = 0
  root_A = isqrt(root_2n / x_max)

  if verbose:
    print 'sieving for smooths...'
  while True:
    # find an integer value A such that:
    # A is =~ sqrt(2*n) / x_max
    # A is a perfect square
    # sqrt(A) is prime, and n is a quadratic residue mod sqrt(A)
    while True:
      root_A = next_prime(root_A)
      leg = legendre(n, root_A)
      if leg == 1:
        break
      elif leg == 0:
        if verbose:
          print 'dumb luck found factors:'
          print root_A, 'x', n/root_A
        return root_A

    A = root_A * root_A

    # solve for an adequate B
    # B*B is a quadratic residue mod n, such that B*B-A*C = n
    # this is unsolvable if n is not a quadratic residue mod sqrt(A)
    b = mod_sqrt(n, root_A)
    B = (b + (n - b*b) * mod_inv(b + b, root_A))%A

    # B*B-A*C = n <=> C = (B*B-n)/A
    C = (B*B - n) / A

    num_poly += 1

    # sieve for prime factors
    sums = [0.0]*(2*x_max)
    i = 0
    for p in prime:
      if p < min_prime:
        i += 1
        continue
      logp = log_p[i]

      inv_A = mod_inv(A, p)
      # modular root of the quadratic
      a = int(((mod_root[i] - B) * inv_A)%p)
      b = int(((p - mod_root[i] - B) * inv_A)%p)

      k = 0
      while k < x_max:
        if k+a < x_max:
          sums[k+a] += logp
        if k+b < x_max:
          sums[k+b] += logp
        if k:
          sums[k-a+x_max] += logp
          sums[k-b+x_max] += logp

        k += p
      i += 1

    # check for smooths
    i = 0
    for v in sums:
      if v > thresh:
        x = x_max-i if i > x_max else i
        vec = set()
        sqr = []
        # because B*B-n = A*C
        # (A*x+B)^2 - n = A*A*x*x+2*A*B*x + B*B - n
        #               = A*(A*x*x+2*B*x+C)
        # gives the congruency
        # (A*x+B)^2 = A*(A*x*x+2*B*x+C) (mod n)
        # because A is chosen to be square, it doesn't need to be sieved
        val = sieve_val = A*x*x + 2*B*x + C

        if sieve_val < 0:
          vec = set([-1])
          sieve_val = -sieve_val

        for p in prime:
          while sieve_val%p == 0:
            if p in vec:
              # keep track of perfect square factors
              # to avoid taking the sqrt of a gigantic number at the end
              sqr += [p]
            vec ^= set([p])
            sieve_val = int(sieve_val / p)

        if sieve_val == 1:
          # smooth
          smooth += [(vec, (sqr, (A*x+B), root_A))]
          used_prime |= vec
        elif sieve_val in partial:
          # combine two partials to make a (xor) smooth
          # that is, every prime factor with an odd power is in our factor base
          pair_vec, pair_vals = partial[sieve_val]
          sqr += list(vec & pair_vec) + [sieve_val]
          vec ^= pair_vec
          smooth += [(vec, (sqr + pair_vals[0], (A*x+B)*pair_vals[1], root_A*pair_vals[2]))]
          used_prime |= vec
          num_partial += 1
        else:
          # save partial for later pairing
          partial[sieve_val] = (vec, (sqr, A*x+B, root_A))
      i += 1

    num_smooth = len(smooth)
    num_used_prime = len(used_prime)

    if verbose:
      print 100 * num_smooth / num_prime, 'percent complete\r',

    if num_smooth > num_used_prime:
      if verbose:
        print '%d polynomials sieved (%d values)'%(num_poly, num_poly*x_max*2)
        print 'found %d smooths (%d from partials) in %f seconds'%(num_smooth, num_partial, clock()-time1)
        print 'solving for non-trivial congruencies...'

      used_prime_list = sorted(list(used_prime))

      # set up bit fields for gaussian elimination
      masks = []
      mask = 1
      bit_fields = [0]*num_used_prime
      for vec, vals in smooth:
        masks += [mask]
        i = 0
        for p in used_prime_list:
          if p in vec: bit_fields[i] |= mask
          i += 1
        mask <<= 1

      # row echelon form
      col_offset = 0
      null_cols = []
      for col in xrange(num_smooth):
        pivot = col-col_offset == num_used_prime or bit_fields[col-col_offset] & masks[col] == 0
        for row in xrange(col+1-col_offset, num_used_prime):
          if bit_fields[row] & masks[col]:
            if pivot:
              bit_fields[col-col_offset], bit_fields[row] = bit_fields[row], bit_fields[col-col_offset]
              pivot = False
            else:
              bit_fields[row] ^= bit_fields[col-col_offset]
        if pivot:
          null_cols += [col]
          col_offset += 1

      # reduced row echelon form
      for row in xrange(num_used_prime):
        # lowest set bit
        mask = bit_fields[row] & -bit_fields[row]
        for up_row in xrange(row):
          if bit_fields[up_row] & mask:
            bit_fields[up_row] ^= bit_fields[row]

      # check for non-trivial congruencies
      for col in null_cols:
        all_vec, (lh, rh, rA) = smooth[col]
        lhs = lh   # sieved values (left hand side)
        rhs = [rh] # sieved values - n (right hand side)
        rAs = [rA] # root_As (cofactor of lhs)
        i = 0
        for field in bit_fields:
          if field & masks[col]:
            vec, (lh, rh, rA) = smooth[i]
            lhs += list(all_vec & vec) + lh
            all_vec ^= vec
            rhs += [rh]
            rAs += [rA]
          i += 1

        factor = gcd(list_prod(rAs)*list_prod(lhs) - list_prod(rhs), n)
        if factor != 1 and factor != n:
          break
      else:
        if verbose:
          print 'none found.'
        continue
      break

  if verbose:
    print 'factors found:'
    print factor, 'x', n/factor
    print 'time elapsed: %f seconds'%(clock()-time1)
  return factor

if __name__ == "__main__":
  parser =ArgumentParser(description='Uses a MPQS to factor a composite number')
  parser.add_argument('composite', metavar='number_to_factor', type=long,
      help='the composite number to factor')
  parser.add_argument('--verbose', dest='verbose', action='store_true',
      help="enable verbose output")
  args = parser.parse_args()

  if args.verbose:
    mpqs(args.composite, args.verbose)
  else:
    time1 = clock()
    print mpqs(args.composite)
    print 'time elapsed: %f seconds'%(clock()-time1)

my_math.py

# divide and conquer list product
def list_prod(a):
  size = len(a)
  if size == 1:
    return a[0]
  return list_prod(a[:size>>1]) * list_prod(a[size>>1:])

# greatest common divisor of a and b
def gcd(a, b):
  while b:
    a, b = b, a%b
  return a

# modular inverse of a mod m
def mod_inv(a, m):
  a = int(a%m)
  x, u = 0, 1
  while a:
    x, u = u, x - (m/a)*u
    m, a = a, m%a
  return x

# legendre symbol (a|m)
# note: returns m-1 if a is a non-residue, instead of -1
def legendre(a, m):
  return pow(a, (m-1) >> 1, m)

# modular sqrt(n) mod p
# p must be prime
def mod_sqrt(n, p):
  a = n%p
  if p%4 == 3:
    return pow(a, (p+1) >> 2, p)
  elif p%8 == 5:
    v = pow(a << 1, (p-5) >> 3, p)
    i = ((a*v*v << 1) % p) - 1
    return (a*v*i)%p
  elif p%8 == 1:
    # Shank's method
    q = p-1
    e = 0
    while q&1 == 0:
      e += 1
      q >>= 1

    n = 2
    while legendre(n, p) != p-1:
      n += 1

    w = pow(a, q, p)
    x = pow(a, (q+1) >> 1, p)
    y = pow(n, q, p)
    r = e
    while True:
      if w == 1:
        return x

      v = w
      k = 0
      while v != 1 and k+1 < r:
        v = (v*v)%p
        k += 1

      if k == 0:
        return x

      d = pow(y, 1 << (r-k-1), p)
      x = (x*d)%p
      y = (d*d)%p
      w = (w*y)%p
      r = k
  else: # p == 2
    return a

#integer sqrt of n
def isqrt(n):
  c = n*4/3
  d = c.bit_length()

  a = d>>1
  if d&1:
    x = 1 << a
    y = (x + (n >> a)) >> 1
  else:
    x = (3 << a) >> 2
    y = (x + (c >> a)) >> 1

  if x != y:
    x = y
    y = (x + n/x) >> 1
    while y < x:
      x = y
      y = (x + n/x) >> 1
  return x

# strong probable prime
def is_sprp(n, b=2):
  if n < 2: return False
  d = n-1
  s = 0
  while d&1 == 0:
    s += 1
    d >>= 1

  x = pow(b, d, n)
  if x == 1 or x == n-1:
    return True

  for r in xrange(1, s):
    x = (x * x)%n
    if x == 1:
      return False
    elif x == n-1:
      return True

  return False

# lucas probable prime
# assumes D = 1 (mod 4), (D|n) = -1
def is_lucas_prp(n, D):
  P = 1
  Q = (1-D) >> 2

  # n+1 = 2**r*s where s is odd
  s = n+1
  r = 0
  while s&1 == 0:
    r += 1
    s >>= 1

  # calculate the bit reversal of (odd) s
  # e.g. 19 (10011) <=> 25 (11001)
  t = 0
  while s:
    if s&1:
      t += 1
      s -= 1
    else:
      t <<= 1
      s >>= 1

  # use the same bit reversal process to calculate the sth Lucas number
  # keep track of q = Q**n as we go
  U = 0
  V = 2
  q = 1
  # mod_inv(2, n)
  inv_2 = (n+1) >> 1
  while t:
    if t&1:
      # U, V of n+1
      U, V = ((U + V) * inv_2)%n, ((D*U + V) * inv_2)%n
      q = (q * Q)%n
      t -= 1
    else:
      # U, V of n*2
      U, V = (U * V)%n, (V * V - 2 * q)%n
      q = (q * q)%n
      t >>= 1

  # double s until we have the 2**r*sth Lucas number
  while r:
    U, V = (U * V)%n, (V * V - 2 * q)%n
    q = (q * q)%n
    r -= 1

  # primality check
  # if n is prime, n divides the n+1st Lucas number, given the assumptions
  return U == 0

# primes less than 212
small_primes = set([
    2,  3,  5,  7, 11, 13, 17, 19, 23, 29,
   31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
   73, 79, 83, 89, 97,101,103,107,109,113,
  127,131,137,139,149,151,157,163,167,173,
  179,181,191,193,197,199,211])

# pre-calced sieve of eratosthenes for n = 2, 3, 5, 7
indices = [
    1, 11, 13, 17, 19, 23, 29, 31, 37, 41,
   43, 47, 53, 59, 61, 67, 71, 73, 79, 83,
   89, 97,101,103,107,109,113,121,127,131,
  137,139,143,149,151,157,163,167,169,173,
  179,181,187,191,193,197,199,209]

# distances between sieve values
offsets = [
  10, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6,
   6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4,
   2, 4, 8, 6, 4, 6, 2, 4, 6, 2, 6, 6,
   4, 2, 4, 6, 2, 6, 4, 2, 4, 2,10, 2]

max_int = 2147483647

# an 'almost certain' primality check
def is_prime(n):
  if n < 212:
    return n in small_primes

  for p in small_primes:
    if n%p == 0:
      return False

  # if n is a 32-bit integer, perform full trial division
  if n <= max_int:
    i = 211
    while i*i < n:
      for o in offsets:
        i += o
        if n%i == 0:
          return False
    return True

  # Baillie-PSW
  # this is technically a probabalistic test, but there are no known pseudoprimes
  if not is_sprp(n, 2): return False

  # idea shamelessly stolen from Mathmatica
  # if n is a 2-sprp and a 3-sprp, n is necessarily square-free
  if not is_sprp(n, 3): return False

  a = 5
  s = 2
  # if n is a perfect square, this will never terminate
  while legendre(a, n) != n-1:
    s = -s
    a = s-a
  return is_lucas_prp(n, a)

# next prime strictly larger than n
def next_prime(n):
  if n < 2:
    return 2
  # first odd larger than n
  n = (n + 1) | 1
  if n < 212:
    while True:
      if n in small_primes:
        return n
      n += 2

  # find our position in the sieve rotation via binary search
  x = int(n%210)
  s = 0
  e = 47
  m = 24
  while m != e:
    if indices[m] < x:
      s = m
      m = (s + e + 1) >> 1
    else:
      e = m
      m = (s + e) >> 1

  i = int(n + (indices[m] - x))
  # adjust offsets
  offs = offsets[m:] + offsets[:m]
  while True:
    for o in offs:
      if is_prime(i):
        return i
      i += o

---

Sample I/O:

$ pypy mpqs.py --verbose 94968915845307373740134800567566911
smoothness bound: 6117
sieve size: 24360
log threshold: 14.3081031579
skipping primes less than: 47
sieving for smooths...
144 polynomials sieved (7015680 values)
found 405 smooths (168 from partials) in 0.513794 seconds
solving for non-trivial congruencies...
factors found:
216366620575959221 x 438925910071081891
time elapsed: 0.685765 seconds

$ pypy mpqs.py --verbose 523022617466601111760007224100074291200000001
smoothness bound: 9998
sieve size: 37440
log threshold: 15.2376302725
skipping primes less than: 59
sieving for smooths...
428 polynomials sieved (32048640 values)
found 617 smooths (272 from partials) in 1.912131 seconds
solving for non-trivial congruencies...
factors found:
14029308060317546154181 x 37280713718589679646221
time elapsed: 2.064387 seconds

Note: not using the --verbose option will give slightly better timings:

$ pypy mpqs.py 94968915845307373740134800567566911
216366620575959221
time elapsed: 0.630235 seconds

$ pypy mpqs.py 523022617466601111760007224100074291200000001
14029308060317546154181
time elapsed: 1.886068 seconds

---

Basic Concepts

In general, a quadratic sieve is based on the following observation: any odd composite n may be represented as:

This is not very difficult to confirm. Since n is odd, the distance between any two cofactors of n must be even 2d, where x is the mid point between them. Moreover, the same relation holds for any multiple of n

Note that if any such x and d can be found, it will immediately result in a (not necessarily prime) factor of n, since x + d and x - d both divide n by definition. This relation can be further weakened - at the consequence of allowing potential trivial congruencies - to the following form:

So in general, if we can find two perfect squares which are equivalent mod n, then it's fairly likely that we can directly produce a factor of n a la gcd(x ± d, n). Seems pretty simple, right?

Except it's not. If we intended to conduct an exhaustive search over all possible x, we would need to search the entire range from [√n, √(2n)], which is marginally smaller than full trial division, but also requires an expensive is_square operation each iteration to confirm the value of d. Unless it is known beforehand that n has factors very near √n, trial division is likely to be faster.

Perhaps we can weaken this relation even more. Suppose we chose an x, such that for

a full prime factorization of y is readily known. If we had enough such relations, we should be able to construct an adequate d, if we choose a number of y such that their product is a perfect square; that is, all prime factors are used an even number of times. In fact, if we have more such y than the total number of unique prime factors they contain, a solution is guaranteed to exist; It becomes a system of linear equations. The question now becomes, how do we chose such x? That's where sieving comes into play.

The Sieve

Consider the polynomial:

Then for any prime p and integer k, the following is true:

This means that after solving for the roots of the polynomial mod p - that is, you've found an x such that y(x) ≡ 0 (mod p), ergo y is divisible by p - then you have found an infinite number of such x. In this way, you can sieve over a range of x, identifying small prime factors of y, hopefully finding some for which all prime factors are small. Such numbers known as k-smooth, where k is the largest prime factor used.

There's a few problems with this approach, though. Not all values of x are adequate, in fact, there's only very few of them, centered around √n. Smaller values will become largely negative (due to the -n term), and larger values will become too large, such that it is unlikely that their prime factorization consists only of small primes. There will be a number of such x, but unless the composite you're factoring is very small, it's highly unlikely that you'll find enough smooths to result in a factorization. And so, for larger n, it becomes necessary to sieve over multiple polynomials of a given form.

Multiple Polynomials

So we need more polynomials to sieve? How about this:

That'll work. Note that A and B could literally be any integer value, and the math still holds. All we need to do is choose a few random values, solve for the root of the polynomial, and sieve the values close to zero. At this point we could just call it good enough: if you throw enough stones in random directions, you're bound to break a window sooner or later.

Except, there's a problem with that too. If the slope of the polynomial is large at the x-intercept, which it will be if it isn't relatively flat, there'll only be a few suitable values to sieve per polynomial. It'll work, but you'll end up sieving a whole lot of polynomials before you get what you need. Can we do better?

We can do better. An observation, as a result of Montgomery is as follows: if A and B are chosen such that there exists some C satisfying

then the entire polynomial can be rewritten as

Furthermore, if A is chosen to be a perfect square, the leading A term can be neglected while sieving, resulting in much smaller values, and a much flatter curve. For such a solution to exist, n must be a quadratic residue mod √A, which can be known immediately by computing the Legendre symbol:
(n | √A) = 1. Note that in order to solve for B, a complete prime factorization of √A needs to be known (in order to take the modular square root √n (mod √A)), which is why √A is typically chosen to be prime.

It can then be shown that if 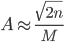, then for all values of x ∈ [-M, M]:

And now, finally, we have all the components necessary to implement our sieve. Or do we?

Powers of Primes as Factors

Our sieve, as described above, has one major flaw. It can identify which values of x will result in a y divisible by p, but it cannot identify whether or not this y is divisible by a power of p. In order to determine that, we would need to perform trial division on the value to be sieved, until it is no longer divisible by p. We seemed to have reached an impassé: the whole point of the sieve was so that we didn't have to do that. Time to check the playbook.

That looks pretty useful. If the sum of the ln of all of the small prime factors of y is close to the expected value of ln(y), then it's almost a given that y has no other factors. In addition, if we adjust the expected value down a little bit, we can also identify values as smooth which have several powers of primes as factors. In this way, we can use the sieve as a 'pre-screening' process, and only factor those values which are likely to be smooth.

This has a few other advantages as well. Note that small primes contribute very little to the ln sum, but yet they require the most sieve time. Sieving the value 3 requires more time than 11, 13, 17, 19, and 23 combined. Instead, we can just skip the first few primes, and adjust the threshold down accordingly, assuming a certain percentage of them would have passed.

Another result, is that a number of values will be allowed to 'slip through', which are mostly smooth, but contain a single large cofactor. We could just discard these values, but suppose we found another mostly smooth value, with exactly the same cofactor. We can then use these two values to construct a usable y; since their product will contain this large cofactor squared, it no longer needs to be considered.

Putting it all together

The last thing we need to do is to use these values of y construct an adequate x and d. Suppose we only consider the non-square factors of y, that is, the prime factors of an odd power. Then, each y can be expressed in the following manner:

which can be expressed in the matrix form:

The problem then becomes to find a vector v such that vM = ⦳ (mod 2), where ⦳ is the null vector. That is, to solve for the left null space of M. This can be done in a number of ways, the simplest of which is to perform Gaussian Elimination on M^T, replacing the row addition operation with a row xor. This will result in a number of null space basis vectors, any combination of which will produce a valid solution.

The construction of x is fairly straight-forward. It is simply the product of Ax + B for each of the y used. The construction of d is slightly more complicated. If we were to take the product of all y, we will end up with a value with 10s of thousands, if not 100s of thousands of digits, for which we need to find the square root. This calcuation is impractically expensive. Instead, we can keep track of the even powers of primes during the sieving process, and then use and and xor operations on the vectors of non-square factors to reconstruct the square root.

I seem to have reached the 30000 character limit. Ahh well, I suppose that's good enough.

Answer 2

Well, your 38!+1 broke my php script, not sure why. In fact, any semi-prime over 16 digits long breaks my script.

However, using 8980935344490257 ( 86028157 * 104395301 ) my script managed a time of 25.963 seconds on my home computer (2.61GHz AMD Phenom 9950). A lot faster than my work computer which was nearly 31 seconds @ 2.93GHz Core 2 Duo.

php - 757 chars incl. new lines

<?php
function getTime() {
    $t = explode( ' ', microtime() );
    $t = $t[1] + $t[0];
    return $t;
}
function isDecimal($val){ return is_numeric($val) && floor($val) != $val;}
$start = getTime();
$semi_prime = 8980935344490257;
$slice      = round(strlen($semi_prime)/2);
$max        = (pow(10, ($slice))-1);
$i          = 3;
echo "\nFactoring the semi-prime:\n$semi_prime\n\n";

while ($i < $max) {
    $sec_factor = ($semi_prime/$i);
    if (isDecimal($sec_factor) != 1) {
        $mod_f = bcmod($i, 1);
        $mod_s = bcmod($sec_factor, 1);
        if ($mod_f == 0 && $mod_s == 0) {
            echo "First factor = $i\n";
            echo "Second factor = $sec_factor\n";
            $end=getTime();
            $xtime=round($end-$start,4).' seconds';
            echo "\n$xtime\n";
            exit();
        }
    }
    $i += 2;
}
?>

I'd be interested to see this same algorithm in c or some other compiled language.