Rotate a hypercube

Question

Introduction

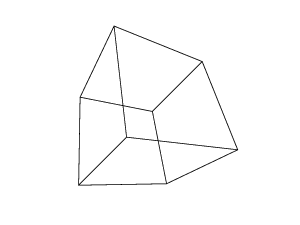
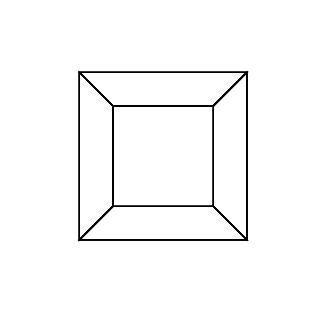
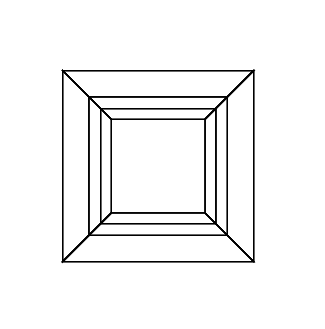
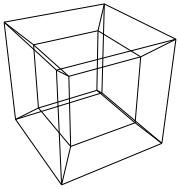
A hypercube/tesseract is the 4 dimensional equivalent of a normal cube. It's made by taking a cube net, extending it to the 3rd dimension, then – using the 4th dimension – folding it into a hypercube. It's basically a cube, where each side is a cube.

To create a hypercube, you need 16 4d vectors (a vector with an x, a y, a z and a w component). These vectors are the following:

A(0, 0, 0, 0); B(1, 0, 0, 0); C(1, 0, 1, 0); D(0, 0, 1, 0); E(0, 1, 0, 0); F(1, 1, 0, 0); G(1, 1, 1, 0); H(0, 1, 1, 0); 
I(0, 0, 0, 1); J(1, 0, 0, 1); K(1, 0, 1, 1); L(0, 0, 1, 1); M(0, 1, 0, 1); N(1, 1, 0, 1); O(1, 1, 1, 1); P(0, 1, 1, 1);

The hypercube has 24 faces. The following list contains all of them (every group marks a quad):

ABFE, CDHG, BCGF, DAEH, DCBA, FEHG
IJNM, KLPO, JKON, LIMP, LKJI, PMNO
ABJI, DCKL, BCKJ, DAIL, FEMN, GHPO, FGON, EHPM, EAIM, BFNJ, CGOK, HDLP

With all this information, you technically have a hypercube in code. To rotate this, you need 6 different matrices for each rotational plane, one for the YZ, XZ, XY, XW, YW and ZW planes. After you have every matrix, you need to multiply the cube's vertices with them.

The following images show the structure of each matrix:

For the rotation on the YZ plane:

For the rotation on the XZ plane:

For the rotation on the XY plane:

For the rotation on the XW plane:

For the rotation on the YW plane:

For the rotation on the ZW plane:

The rotations get applied in this order.

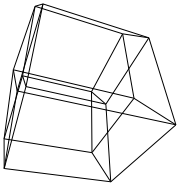
After all this, you have a rotated hypercube. Now you need to draw it. You should use an orthogonal projection combined with a perspective projection to send (x, y, z, w) to (2x/(2+z), 2y/(2+z)).

Input

Your input is 6 integers between 0 (inclusively) and 360 (exclusively). These represent the rotations in degrees on the different rotational planes of the hypercube.

Output

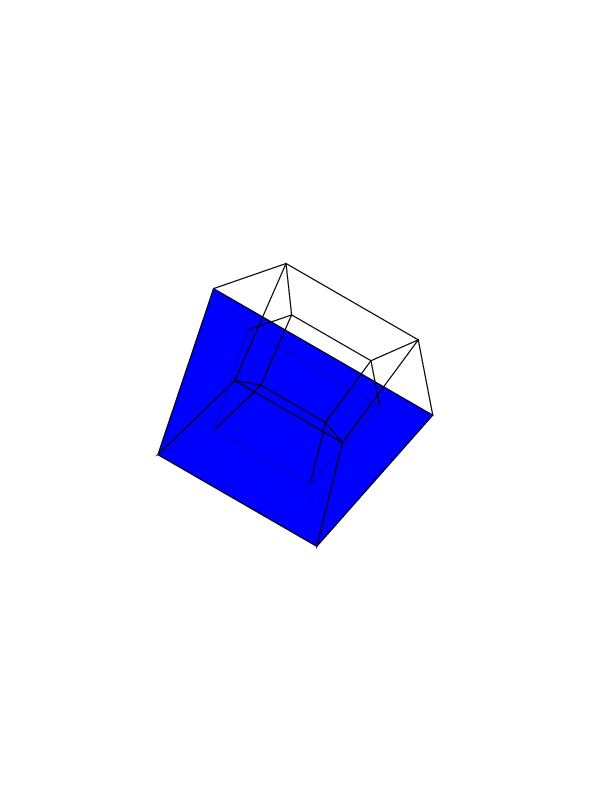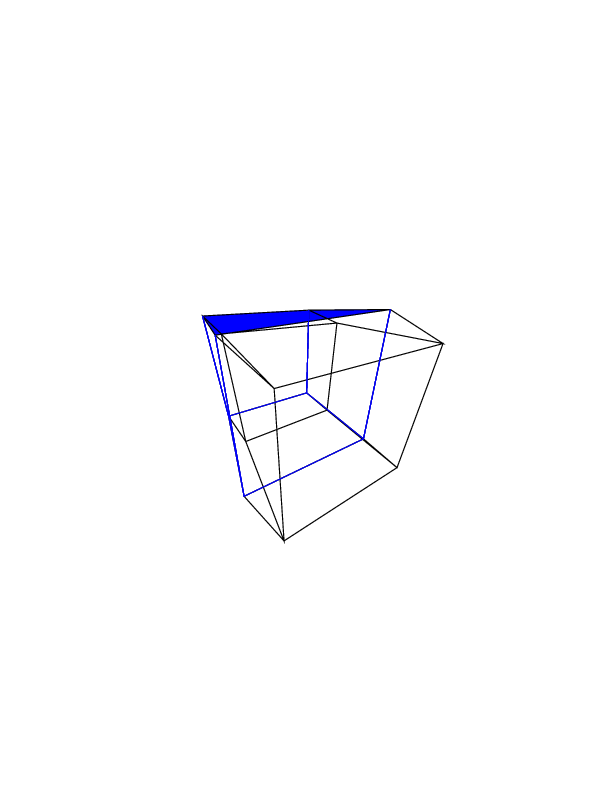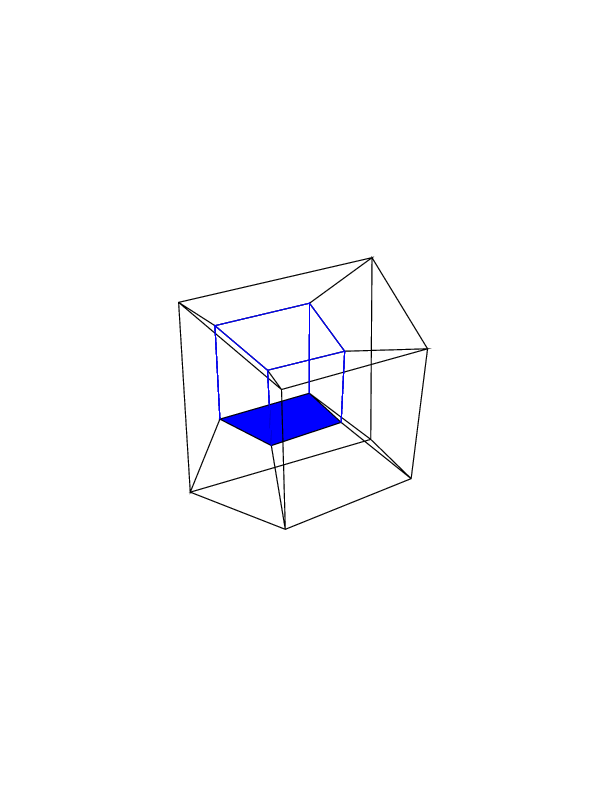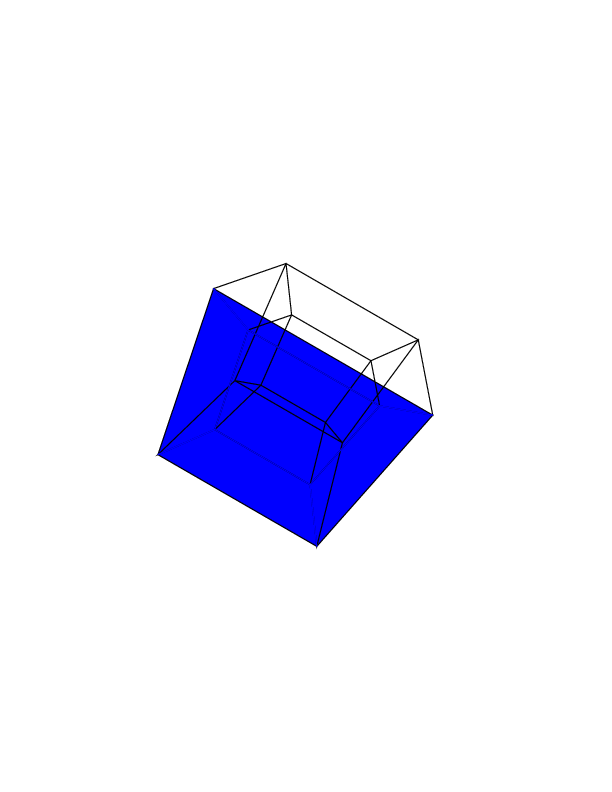
Your output should be a single image containing the hypercube. The display can be a rasterized image, a vector image or an ASCII art. The output image should be at least 100 * 100 pixels, and the cube needs to take up at least 50% of the screen. Any default image output format is allowed.

Test cases

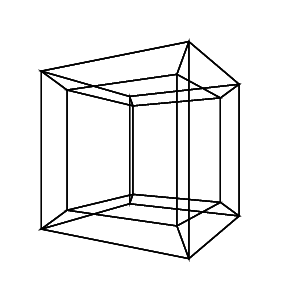
0 0 0 0 0 0

0 0 0 0 0 30

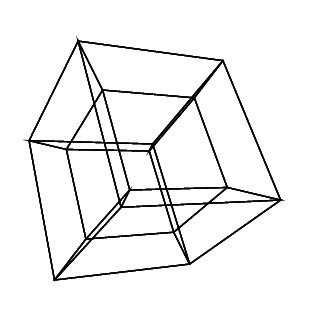
30 0 0 0 0 30

0 0 0 30 30 30

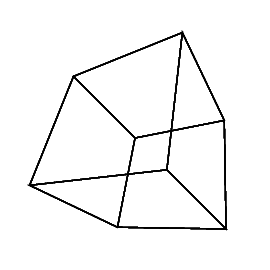
45 45 45 0 0 0

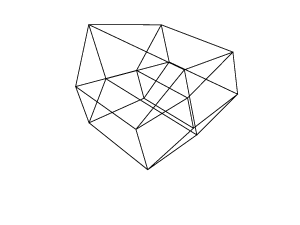
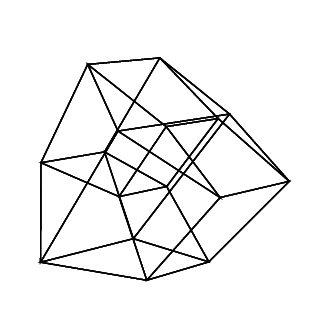
45 45 45 45 45 45

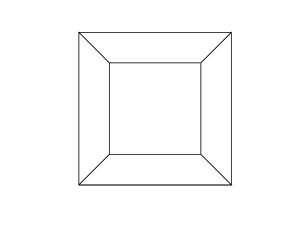
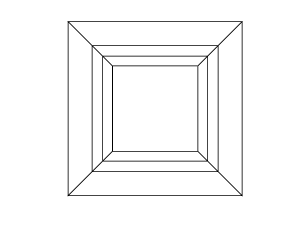
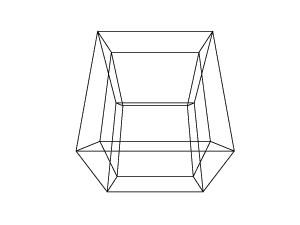
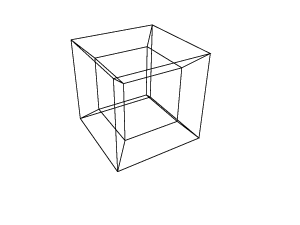
Open the images in a new tab, to see them in full size.

Rules

• Default rules apply
• Standard loopholes are forbidden
• Shortest code in bytes wins

Answer 1

Octave, 474 433 429 bytes

function H(a,b,c,d,e,f) C=@cosd;S=@sind;R=[1,0,0,0;0,C(e),0,-S(e);0,-S(e)*S(f),C(f),-C(e)*S(f);0,S(e)*C(f),S(f),C(e)*C(f)]*[C(c)*C(d),-S(c)*C(d),0,S(d);S(c),C(c),0,0;0,0,1,0;-C(c)*S(d),S(c)*S(d),0,C(d)]*[C(b),S(a)*S(b),C(a)*S(b),0;0,C(a),-S(a),0;-S(b),S(a)*C(b),C(a)*C(b),0;0,0,0,1]*(dec2bin(0:15)'-48.5);Z=R(3,:)+2;R=2*R./Z;Q=[1,2,10,12,11,9,10,14,16,12,4,8,16,15,11,3,7,15,13,9,1,5,13,14,6,8,7,5,6,2,4,3,1];plot(R(1,Q),R(2,Q));

Rotated:

function H(a,b,c,d,e,f) 
C=@cosd;S=@sind;
R=[1,0,0,0;0,C(e),0,-S(e);0,-S(e)*S(f),C(f),-C(e)*S(f);0,S(e)*C(f),S(f),C(e)*C(f)]*
  [C(c)*C(d),-S(c)*C(d),0,S(d);S(c),C(c),0,0;0,0,1,0;-C(c)*S(d),S(c)*S(d),0,C(d)]*
  [C(b),S(a)*S(b),C(a)*S(b),0;0,C(a),-S(a),0;-S(b),S(a)*C(b),C(a)*C(b),0;0,0,0,1]*
  (dec2bin(0:15)'-48.5);
Z=R(3,:)+2;
R=2*R./Z;
Q=[1,2,10,12,11,9,10,14,16,12,4,8,16,15,11,3,7,15,13,9,1,5,13,14,6,8,7,5,6,2,4,3,1];
plot(R(1,Q),R(2,Q));

The rotation matrices still consume a lot of bytes, but the Eulerian cycle worked out quite well, reducing the number of vertices visited from 96 120 down to 33.

Vertices are generated by taking the 4-bit binary representation of [0:15] and considering the msb to be the x-coordinate and the lsb the w-coordinate.

Edit: Pre-multiplying all of the rotation matrices was a nightmare, which is why I didn't use it initially, but pre-multiplying them in pairs saved 41 bytes. Now to look for the optimum combination. :) Multiplying the matrices by threes was worse than no pre-multiplication at all, so I'll be happy with the pair-wise approach.

---

Output:

H(0,0,0,0,0,0)

H(0,0,0,0,0,30)

H(30,0,0,0,0,30)

H(0,0,0,30,30,30)

H(45,45,45,0,0,0)

H(45,45,45,45,45,45)

Answer 2

Postscript 1075 732 683 640 631 601 590 545 542 526 514 478 470

Uses mat.ps and G.

Edit:-343 Applied binary-encoding generation of vectors and Eulerian circuit stolen borrowed from other answers. And applied binary-token-strings from the G library.
Edit:-49 Redefined sin cos and neg to shorter names.
Edit:-43 Defined short names for sequences 0 0 0 1 1 0.
Edit:-9 al (ie. aload) is shorter than (")@. Factored 3 calls to idi (ie. idiv) at the cost of a do-nothing 1 idiv.
Edit:-30 Applied implicit definition block from G.
Edit:-10 A few more triply-used sequences.
Edit:-45 Remove variables i j k l m n for the angles and always define the current angle as t and functions of angles use the value of the (global) t variable. Defer execution of the code-description of the rotation matrix until its t value is ready.
Edit:-3 Remove <16>$ ie. closepath. And a space.
Edit:-16 Factor-out array brackets from unit vectors in the rotation matrices (J K L and M). Re-apply dropped mo for mod and su for sub.
Edit:-12 In-line the project-and-draw function and remove (now empty) enclosing dictionary.
Edit:-36 Encoded the circuit (ie. the faces) in a string.
Edit:-8 Remove definition of vertices array V. Instead, leave on stack and dup working copies as needed (once, at first, and again at the end of the loop). Also, translated a few operators from binary-token-strings back to abbreviated names where the BTS gave no savings, so (I)$ is now fora (ie. forall). if du could be (T8)$, but if du is clearly a better choice (it's golf, not obfuscation per se). Also, perform the scale before translate, so translated coordinates can be 3 and 4 instead of 300 and 400.

(mat.ps)run 3(G)run $
t sin
A neg
t cos
0 0
0 1
1 0
2 mu Z 2(!V)@
idi 2 mo .5 su
(>8)$
[F D]
[D E]
[E D]
[D F]

3 4 100(&>88)$(,)# div(<N)#[E 15{[I 1 H I 2 H I 4 H ex 8 H]}fo]E
5{ARGUMENTS 1(XK/)$/t ex d{{J[0 C B 0][0 A C 0]K}{[C 0 A 0]L[B 0
C 0]K}{[C B D][A C D]M K}{[C D A]L M[B D C]}{J[0 C 0 B]M[0 A 0
C]}{J L[D C B][D A C]}}(>K)$[(>?)$]transpose matmul}fo
du(019;:89=?;37?>:26><804<=576451320){48 su get al po{W
Z Y X}{(>3)$}fora X G Y G{li}(D)#{mov}if du}fora(HB)#

The 3 4 and 100 in the first line of the second block are parameters representing center-x, center-y and scale, respectively, of the drawing on the page (center coordinates are scaled by scale). (300,400) is roughly the center of US letter-sized paper (612,792) in PS units.

If you can roughly follow postscript, the important bizarre things are the implicit procedure block and the encoded operator strings. As shown by comments in the workfile, below, each line of the first block is implicitly named by A, B, C, etc. So, eg. F E D would produce 1 0 0 1 0 0. For the encoded operator strings, anything that is an argument to $ # or @ is a sequence of operator calls, using the bytes to select operators from the system name table, PLRM 3ed Appendix F. These features and more are available for PostScript with the G library (now includes the mat.ps functions too).

Workfile:

(mat.ps)run 3(G)run $
t sin %/A
A neg %/B
t cos %/C
0 0 %/D
0 1 %/E
1 0 %/F
2 mu Z 2(!V)@ %/G  %ad div %add div %108 1 54
idi 2 mo .5 su %idiv mod sub %/H %106 169 51
(>8)$ %/I %exch dup
[F D] %/J
[D E] %/K
[E D] %/L
[D F] %/M


3 4
100(&>88)$ %currentlinewidth exch dup dup %38
(,)#  %scale %139-95=44
div(<N)# %div setlinewidth %54 155-95=60 %translate %173-95=78
%/V
[E 15{[ I
    1 H I
    2 H I
    4 H ex
    8 H]}fo]

E 5{ARGUMENTS 1(XK/)$ %index get cvr %88 75 47
    /t ex d %exch def %62 51
    {{J[0 C B 0][0 A C 0]K} 
     {[C 0 A 0]L[B 0 C 0]K} 
     {[C B D][A C D]M K} 
     {[C D A]L M[B D C]}
     {J[0 C 0 B]M[0 A 0 C]}
     {J L[D C B][D A C]}}
    (>K)$ %exch get %62 75
    [
        (>?)$ %exch exec %62 63
    ]
    transpose matmul
}fo %for
du %dup
%d %def
%{transpose matmul}fora d

%[E 9 11 10 8 9 13 15 11 3 7 15 14 10 2 6 14 12 8 0 4 12 13 5 7 6 4 5 1 3 2 0]
%<0001090b0a08090d0f0b03070f0e0a02060e0c0800040c0d050706040501030200>
%          abcdef
%0123456789:;<=>?
(019;:89=?;37?>:26><804<=576451320)
{48 su get % 169 75 %V (>K)$ %sub %exch get

    al po %aload pop %2 117
    {W Z Y X}{(>3)$ %exch def
    }fora %forall %2 117  62 51 73
    X G
    Y G
    {li}(D)# %stopped
    {mov}
    if du%(T8)$ %if %84 du %dup 56
}
%<49a7a1>$ %forall stroke showpage %73 167-95=72 161-95=66
fora(HB)#

Ungolfed and lightly commented:

300 400 translate   %roughly center of letter paper
currentlinewidth
100 dup dup scale
div setlinewidth    %scale x100, reduce line-width/100
(mat.ps)run         %load matrix library
ARGUMENTS aload pop{f e d c b a}{exch cvr def}forall  %define args as 
                                 % a,b,etc and convert to real numbers
/m{2 mod .5 sub}def
/P{aload pop{w z y x}{exch def}forall   %P: [x y z w]  project-and-draw  -
    x 2 mul z 2 add div 
    y 2 mul z 2 add div 
    {lineto}stopped{moveto}if %catch(&handle!) nocurrentpoint error in lineto
}bind def
/V[0 1 15{    % generate vectors with a for-loop
    [ exch
        dup m
        1 index 2 idiv m
        2 index 4 idiv m
        4 3 roll 8 idiv m
    ]
}for]
[[[1 0 0 0][0 a cos a sin neg 0][0 a sin a cos 0][0 0 0 1]] 
     [[b cos 0 b sin 0][0 1 0 0][b sin neg 0 b cos 0][0 0 0 1]] 
     [[c cos c sin neg 0 0][c sin c cos 0 0][0 0 1 0][0 0 0 1]] 
     [[d cos 0 0 d sin][0 1 0 0][0 0 1 0][d sin neg 0 0 d cos]]
     [[1 0 0 0][0 e cos 0 e sin neg][0 0 1 0][0 e sin 0 e cos]]
     [[1 0 0 0][0 1 0 0][0 0 f cos f sin neg][0 0 f sin f cos]]]
{transpose matmul} forall def   % apply array of rotations and define

%Eulerian circuit (borrowed and adjusted for 0-based indexing)
[0 1 9 11 10 8 9 13 15 11 3 7 15 14 10 2 6 14 12 8 0 4 12 13 5 7 6 4 5 1 3 2 0]

% the main program!
% on the stack is the Eulerian circuit array
{
    V exch get  %lookup index in (sextuply-transformed) vertex array
    P           %call project-and-draw
} forall
closepath stroke %draw it, don't just think about it

showpage % gs's cmd-line-args option automatically sets -dBATCH,
    % so without a showpage, gs will immediately exit before you
    % can look at the picture :(

Some of my outputs are mirror images of the question's examples.

For gs -- hc.ps 0 0 0 0 0 0, I get:

gs -- hc.ps 0 0 0 0 0 30

gs -- hc.ps 30 0 0 0 0 30

gs -- hc.ps 0 0 0 30 30 30

gs -- hc.ps 45 45 45 0 0 0

gs -- hc.ps 45 45 45 45 45 45

Bonus animation I just made with this program. This image corresponds to the rotation sequence 0 30 60 0 i i, where i ranges from 0 to 360 by 2.

Answer 3

C# + Unity, 1060 845 835 bytes

C# ≈ Java

Assumes that this function is in a script placed on MainCamera.

Edit:
Thanks to @TuukkaX for the suggestions to save 19 bytes Saved ~200 bytes using the Eulerian cycle.

Golfed:

void d(float[]r){transform.position=Vector3.back*2;GetComponent<Camera>().backgroundColor=Color.black;Vector4[]p=new Vector4[16];Matrix4x4[]m=new Matrix4x4[6];int i=0;for(;i<16;i++)p[i]=new Vector4(i%2,i/2%2,i/4%2,i/8%2)-new Vector4(.5f,.5f,.5f,.5f);int[,]X={{6,8,1,12,7,11},{5,0,0,0,5,10},{10,10,5,15,15,15}};for(i=0;i<6;i++){m[i]=Matrix4x4.identity;r[i]=Mathf.Deg2Rad*r[i];float c=Mathf.Cos(r[i]),s=Mathf.Sin(r[i]);m[i][X[1,i]]=c;m[i][X[2,i]]=c;m[i][X[0,i]]=s;m[i][X[0,i]%4*4+X[0,i]/4]=-s;}for(i=0;i<16;i++)foreach(Matrix4x4 x in m)p[i]=x*p[i];int[]F={0,1,9,11,10,8,9,13,15,11,3,7,15,14,10,2,6,14,12,8,0,4,12,13,5,7,6,4,5,1,3,2,0};LineRenderer l=new GameObject().AddComponent<LineRenderer>();l.SetVertexCount(33);l.material=new Material(Shader.Find("Sprites/Default"));l.SetWidth(.03f,.03f);for(i=0;i<33;i++)l.SetPosition(i,p[F[i]]);

Newlines + indentation + Full shell:

using UnityEngine;
using System.Collections;

public class h : MonoBehaviour {

    void d(float[]r)
    {
        transform.position=Vector3.back*2.5f;
        GetComponent<Camera>().backgroundColor=Color.black;
        Vector4[]p=new Vector4[16];
        Matrix4x4[]m=new Matrix4x4[6];
        int i=0;
        for(;i<16;i++)p[i]=new Vector4(i%2,i/2%2,i/4%2,i/8%2)-new Vector4(.5f,.5f,.5f,.5f);
        int[,]X={{6,8,1,12,7,11},{5,0,0,0,5,10},{10,10,5,15,15,15}};
        for (i=0;i<6;i++){
            m[i]=Matrix4x4.identity;
            r[i]=Mathf.Deg2Rad*r[i];
            float c=Mathf.Cos(r[i]);
            float s=Mathf.Sin(r[i]);
            m[i][X[1,i]]=c;
            m[i][X[2,i]]=c;
            m[i][X[0,i]]=s;
            m[i][X[0,i]%4*4+X[0,i]/4]=-s;
        }
        for (i=0;i<16;i++)foreach(Matrix4x4 x in m)p[i]=x*p[i];
        int[]F={0,1,9,11,10,8,9,13,15,11,3,7,15,14,10,2,6,14,12,8,0,4,12,13,5,7,6,4,5,1,3,2,0};
        LineRenderer l=new GameObject().AddComponent<LineRenderer>();
        l.SetVertexCount(33);
        l.material=new Material(Shader.Find("Sprites/Default"));
        l.SetWidth(.03f,.03f);
        for (i=0;i<33;i++)
            l.SetPosition(i,p[F[i]]);
        l.gameObject.tag = "Player";
    }
    public float[] input;
    void Start()
    {
        d(input);
    }
}

I couldn't figure out a simple formula for constructing the rotation matrices nor the "faces" which to draw, so that cost a lot of bytes to hard-code. I borrowed the Eulerian cycle from @beaker. Also, Unity built-ins are extremely verbose.

You can verify all test cases online.

Answer 4

Javascript ES6, 584 bytes

f=(...R)=>(P=s=>[...s].map(i=>parseInt(i,16)),C=document.createElement`canvas`,X=C.getContext`2d`,X.translate((C.width=300)/2,(C.height=300)/2),X.lineWidth=0.01,X.scale(100,100),X.beginPath(),P("0267fd9804c8ab915dcefb37546ea2310").map((e,i)=>{[x,y,z]=P("084c2a6e195d3b7f").map(i=>[...(1e3+i.toString(2)).slice(-4)].map(i=>i-0.5)).map(e=>(R.map((R,i,_,M=Math,C=M.cos(r=R*M.PI/180),S=M.sin(r))=>((a,b,s=1)=>[e[a],e[b]]=[C*e[a]-s*S*e[b],s*S*e[a]+C*e[b]])(...[[1,2],[0,2,-1],[0,1],[0,3,-1],[1,3],[2,3]][i])),e))[e];[x,y]=[2*x/(2+z),2*y/(2+z)];i?X.lineTo(x,y):X.moveTo(x,y)}),X.stroke(),C)

"Ungolfed":

f=(...R)=>(                                                              // function that accepts rotations in the following form: f(a,b,c,d,e,f)
    P=s=>[...s].map(i=>parseInt(i,16)),                                  // function to convert strings to hex-arrays
    V=P("084c2a6e195d3b7f")                                              // vertices encoded as hex values ( [0,1,1,0] -> 6 )
        .map(i=>[...(1e3+i.toString(2)).slice(-4)].map(i=>i-0.5))        // convert hex values to vertices, center the hypercube
        .map(e=>(R.map((R,i,_,M=Math,C=M.cos(r=R*M.PI/180),S=M.sin(r))=> // convert angles to degrees, precalculate sin and cos values
        ((a,b,s=1)=>[e[a],e[b]]=[C*e[a]-s*S*e[b],s*S*e[a]+C*e[b]])       // apply matrix transforms to all vertices
        (...[[1,2],[0,2,-1],[0,1],[0,3,-1],[1,3],[2,3]][i])),e)),        // list of encoded matrix transforms
    C=document.createElement`canvas`,X=C.getContext`2d`,                 // create image to draw on
    X.translate((C.width=300)/2,(C.height=300)/2),                       // setup image dimensions, center transform
    X.lineWidth=0.01,X.scale(100,100),X.beginPath(),                     // setup line, scale the transform and begin drawing
    P("0267fd9804c8ab915dcefb37546ea2310").map((e,i)=>{                  // hypercube edge path indices encoded as hex values
        [x,y,z]=V[e];[x,y]=[2*x/(2+z),2*y/(2+z)];                        // project vertex
        i?X.lineTo(x,y):X.moveTo(x,y)}),X.stroke(),                      // draw vertex
    C)                                                                   // return image

See it in action (modified to continuously rotate):

with(document)with(Math)with(document.getElementById`canvas`)with(getContext`2d`){render=()=>{requestAnimationFrame(render);clearRect(0,0,width,height);save();K=performance.now();R=[K*0.01,K*0.02,K*0.03,K*0.04,K*0.05,K*0.06];X=s=>[...s].map(i=>parseInt(i,16));V=X("084c2a6e195d3b7f").map(i=>[...(1e3+i.toString(2)).slice(-4)].map(i=>i-0.5)).map(e=>(R.map((R,i,_,C=cos(r=R*PI/180),S=sin(r))=>((a,b,s=1)=>[e[a],e[b]]=[C*e[a]-s*S*e[b],s*S*e[a]+C*e[b]])(...[[1,2],[0,2,-1],[0,1],[0,3,-1],[1,3],[2,3]][i])),e));translate((width=300)/2,(height=300)/2);lineWidth=0.01;scale(100,100);beginPath();X("0267fd9804c8ab915dcefb37546ea2310").map((e,i)=>{[x,y,z]=V[e];[x,y]=[2*x/(2+z),2*y/(2+z)];i?lineTo(x,y):moveTo(x,y)});stroke();restore();};render();}

<html><body><canvas id="canvas"></canvas></body></html>

The function returns a HTML5 canvas object, you need to add it to the page by doing document.body.appendChild(f(0,0,0,0,0,0)) for example.

Currently, the rotations are applied out of order, I'm working on the reordering, but as is, it rotates a hypercube correctly.

Answer 5

Mathematica, 453 415 bytes*

Shortened by using the Eulerian tour and cleaning it all up into a single statement without defining functions in variables. This makes the code slower for some reason. I'm guessing Mathematica reevaluates the functions multiple times now that they are not stored in a variable.

Graphics[Line[Table[{2#/(2+#3),2#2/(2+#3)}&@@Map[Dot@@Table[Table[If[n==m==#2||n==m==#,Cos[#3],If[n==#2&&m==#,If[#2==1&&(#==3||#==4),1,-1]Sin[#3],If[n==#&&m==#2,If[#2==1&&(#==3||#==4),-1,1]Sin[#3],If[n==m,1,0]]]],{n,4},{m,4}]&[k[[1]],k[[2]],a[[k[[3]]]]°],{k,{{4,3,6},{4,2,5},{4,1,4},{2,1,3},{3,1,2},{3,2,1}}}].#&,Tuples[{0,1},4]-.5,{1}][[i]],{i,{1,2,10,12,11,9,10,14,16,12,4,8,16,15,11,3,7,15,13,9,1,5,13,14,6,8,7,5,6,2,4,3,1}}]]]

* I am counting ° and == as single bytes each since they are represented as a single character in Mathematica. I think this is fair since lots of languages use weird character encodings.

Ungolfed with comments. The input is hard coded at the top as a={30,0,0,0,0,30};. I didn't count that toward my score.

a = {45, 45, 45, 45, 45, 45};



(* #2,#-th rotation matrix as a funciton of #3 *)
(* Using the \
#-notation saved 6 bytes over the more common function definition \
notation*)
r = 
  Table[If[n == m == #2 || n == m == #, Cos[#3], 
     If[n == #2 && m == #, 
      If[#2 == 1 && (# == 3 || # == 4), 1, -1] Sin[#3], 
      If[n == # && m == #2, 
       If[#2 == 1 && (# == 3 || # == 4), -1, 1] Sin[#3], 
       If[n == m, 1, 0]]]], {n, 4}, {m, 4}] &;

(* Total rotation matrix. Need six of them. Function of the six \
angles to rotate.*)

u = Dot @@ 
     Table[r[k[[1]], 
       k[[2]], \[Degree]*
        a[[k[[3]]]]], {k, {{4, 3, 6}, {4, 2, 5}, {4, 1, 4}, {2, 1, 
         3}, {3, 1, 2}, {3, 2, 1}}}].# &;



(* List of all vertices of the hypercube *)
t = Tuples[{0, 1}, 4];
t -= .5;
v = Map[u, t, {1}];

(*projection*)
p = {2 #/(2 + #3), 2 #2/(2 + #3)} &;

(*Eulerian tour*)

l = Table[
   p @@ v[[i]], {i, {1, 2, 10, 12, 11, 9, 10, 14, 16, 12, 4, 8, 16, 
     15, 11, 3, 7, 15, 13, 9, 1, 5, 13, 14, 6, 8, 7, 5, 6, 2, 4, 3, 
     1}}];
Graphics[Line[l]]

0 0 0 0 0 30

0 0 0 30 30 30

405 10 -14 -8 -9 205