12
1
For every given degree n it is possible to construct (at least one) an integral polynomial p such that p(k) (p evaluated in k) is the coefficient of the term x^k in the polynomial for all 0 <= k <= n. To make them unique, we require the leading coefficient (the coefficient of x^n) to be positive and minimal.
These polynomials have some interesting properties, you can find some references in the thread that inspired me to do this challenge. You can also find those polynomials in https://oeis.org/A103423
One of the a priori unexpected properties is how the roots behave depending on n:
source (by /u/zorngov and /u/EpicSauceSc2)
Task
Given a nonnegative integer n output the self referential integral polynomial of degree n with minimal positive leading coefficient.
Details
The output can be in any human readable form, as string x^2-x-1, or also as a list of coefficients [1,-1,-1]. (The order of the coefficients can also be the other way around, it just needs to be consistent.)
First few outputs
n=0: 1
n=1: x
n=2: x^2-x-1
n=3: 10*x^3-29*x^2-6*x+19
n=4: 57*x^4-325*x^3+287*x^2+423*x-19
n=5: 12813*x^5-120862*x^4+291323*x^3+44088*x^2-355855*x-227362
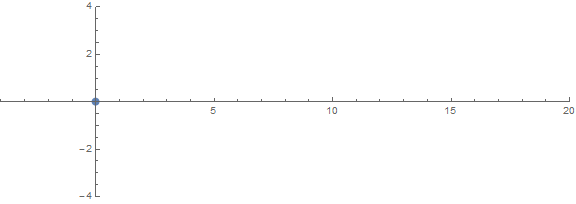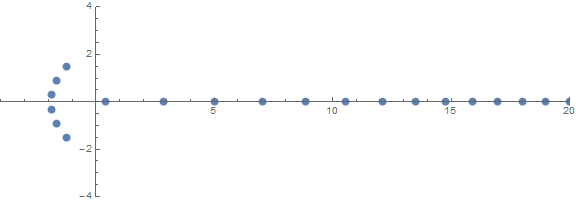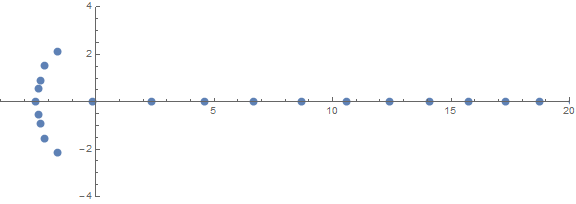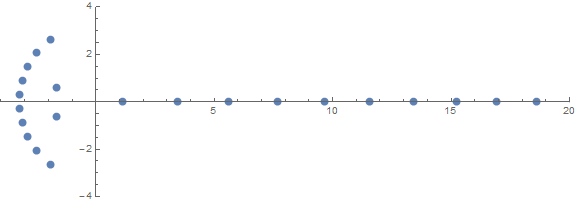
Congrats on your gold badge! – Luis Mendo – 2016-06-01T08:56:23.353
@LuisMendo Thanks, apparently I'm a fanatic. – flawr – 2016-06-01T11:17:16.320