Recursive Steiner Chains

Question

Steiner Chains are a set of N circles where each circle is tangent to 2 other non-intersecting circles as well as the the previous and next circles of the chain, as seen in the below images:

In this challenge, you will write a program/function that draws Steiner chains recursively, that is, circles of a given chain will be the base circles of another iteration of chains:

Challenge

Write a program/function that accepts image dimensions and a list of integers denoting the level of circles in each successive iteration of chains, and output an image with the recursive Steiner chains drawn to it.

Input

Your program/function will accept 2 arguments:

• s - width and height of image
• ls - list of positive integers denoting the number of circles present in each successive iteration of chains, ordered from the top-most chain to the bottom-most chain

Output

Your program/function will output an image of dimension s x s displaying the recusive Steiner chain.

• The top level base circle will be as large as the image with a diameter of s, centered inside the image
• To make things easy, the 2 base circles of a Steiner chain will be concentric, that is, the centerpoints of the 2 baseline circles will be the same
• Given an outer radius, R, and the number of circles in a chain, N, the formula for the inner radius R' is R' = (R-R*sin(pi/N))/(sin(pi/N)+1)
• Circles of the chain as well as the inner base circle will be the outer base circles of the next iteration of chains
• While recursing through the chain circles, the order of the next chain should correspond to the next value in ls
• While recursing through the inner circle of a chain, the order should be the same as its parents order (example [5,2]):
• 
• All chains should end recursion at a depth of the length of ls
• The rotation of the chains doesn't matter:
• 
• However, the rotations of recursive chains relative to their parents centerpoint should be the same:
• 
• All circles should be drawn with an outline or solid fill
• Color choice is left to the implementation, save for loopholes (for example, filling everything with the same color)

Example Runs

In the following examples, color is determined by (depth of the recursion)^4.

You can find source here.

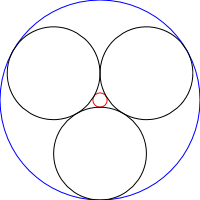
chain(600,[5,4,3])

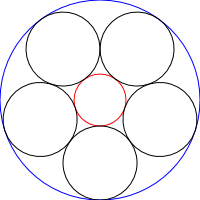
chain(600,[11,1,1,1,1,1,1])

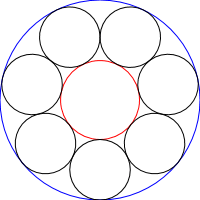
chain(600,[5,6,7,8,9])

Answer 1

Javascript ES6, 379 bytes

This solution was used to generate the example runs in the question.

f=(s,ls)=>{with(V=document.createElement`canvas`)with(getContext`2d`)with(Math)return(width=height=s,translate(s/=2,s),(S=(o,d=0,n=ls[d],i=(o-o*sin(PI/n))/(sin(PI/n)+1),r=0)=>{fillStyle=`rgba(0,0,0,${pow(d/ls.length,4)})`;beginPath(),arc(0,0,o,-PI,PI),fill();if(d++<ls.length){S(i,d,n);for(;r<n;++r){save();translate(0,(o+i)/2);S((o-i)/2,d);restore();rotate((2*PI)/n);}}})(s),V)}

Ungolfed:

f=(s,ls)=>{                                        // define function that accepts image dimensions and a list of orders
 with(V=document.createElement`canvas`)            // create canvas to draw on, bring its functions into current scope chain
 with(getContext`2d`)                              // bring graphics functions into current scope chain
 with(Math)return(                                 // bring Math functions into current scope chain
  width=height=s,                                  // set width and height of image
  translate(s/=2,s),                               // center the transform on image
   (S=(o,d=0,                                      // define recursive function that accepts outer radius, depth, and optionally order
       n=ls[d],                                    // default chain order to corresponding order in input list
       i=(o-o*sin(PI/n))/(sin(PI/n)+1),            // calculate inner base circle radius
       r=0)=>{                                     // initialize for loop var
    fillStyle=`rgba(0,0,0,${pow(d/ls.length,4)})`; // fill based on depth
    beginPath(),arc(0,0,o,-PI,PI),fill();          // draw circle
    if(d++<ls.length){                             // if within recursion limit
     S(i,d,n);                                     //   recurse on inner circle
     for(;r<n;++r){                                //   loop through all circles of the chain
      save();                                      //   save transform
      translate(0,(o+i)/2);                        //   translate origin to middle of the 2 base circles
      S((o-i)/2,d);                                //   recurse on chain circle
      restore();                                   //   restore transform
      rotate((2*PI)/n);                            //   rotate transform to next circle in chain
   }}})(s),                                        // begin the recursion
 V)}                                               // return the canvas

Note: f returns a canvas.

Example run (assumes there's a <body> to append to):

document.body.appendChild(f(600,[13,7,11,5,3]))

Should dump the following image to the page: