33
4
Given an integer N >= 2, produce an image showing a Sierpiński knot of degree N.
For example, here are knots of degree 2, 3, 4 and 5:
Click on the images to view full size (the higher the degree the larger the image).
Specification
- A Sierpiński knot of degree N is drawn using the vertices of a Sierpiński triangle of degree N as guide points. A Sierpiński triangle of degree N is three Sierpiński triangles of degree N-1 arranged into a larger triangle. A Sierpiński triangle of degree 0 is an equilateral triangle.
- The smallest component triangles have side length 64, giving the Sierpiński triangle on which the knot is based an overall side length of

- The centre of the outer triangle is positioned at the centre of the image. This does not give equal white space at top and bottom.
- The output is a square image of side length
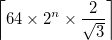 where
where  is
is ceiling(x), the smallest integer greater than or equal to x. This is just large enough for the top vertex of the underlying Sierpiński triangle to be contained within the image when the centre of the triangle is at the centre of the image. - The single curve must pass over and under itself, strictly alternating. Solutions can choose between under then over, or over then under.
- The example images show black foreground and white background. You may choose any two easily distinguished colours. Anti-aliasing is permitted but not necessary.
- There must not be gaps where two arcs meet or where the curve passes over or under itself.
- Output may be to any raster format image file, or to any vector format image file that includes a correct default display size. If you display directly to screen, this must be in a form that allows scrolling to see the full image when larger than the screen.
Determining arc centre, radius and thickness
- The knot is constructed as a series of circular arcs that meet at points where their tangents are parallel, to give a seamless join. These arcs are displayed as annular sectors (arcs with thickness).
- The centres of these arcs are the vertices of the smallest upside down triangles. Each such vertex is the centre of exactly one arc.
- Each arc has a radius of
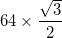
- The exception is that the arcs in the three outermost triangles (at the corners of the large triangle) have a centre which is the midpoint of the two adjacent inner vertices, and thus have a radius of
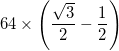
- Each arc is represented with a total thickness (difference between inner radius and outer radius) of
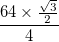 and the black borders of this each have a thickness of
and the black borders of this each have a thickness of 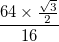 The curve must have these borders, and not just be a solid strip.
The curve must have these borders, and not just be a solid strip.
Units of measure
- All distances are in pixels (1 is the horizontal or vertical distance between 2 adjacent pixels).
- The square root of 3 must be accurate to 7 significant figures. That is, your calculations must be equivalent to using a ROOT3 such that
1.7320505 <= ROOT3 < 1.7320515
Scoring
The shortest code in bytes wins.
For those wondering, N=0 and N=1 are not included because they correspond to a circle and a trefoil, which don't quite match the pattern that applies for N>=2. I would expect that most approaches to this challenge would need to add special case code for 0 and 1, so I decided to omit them.
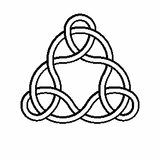
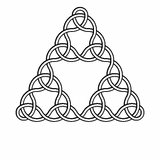




1Would it help to have a diagram to show what all the numbers relate to? – trichoplax – 2016-05-10T11:42:14.090
Before I golf my answer / add corners, are 7 significant figures really necessary for small details like the thickness of the line, etc? An accuracy like "7 significant figures or 1 pixel, whichever is larger" seems more appropriate. – Level River St – 2016-05-15T12:48:49.420
@LevelRiverSt since the size of the image scales with the input, even 7 significant figures is insufficient for 1 pixel accuracy for larger N. I've settled on 7 significant figures after some discussion in chat, so that all answers are held to the same standard. – trichoplax – 2016-05-15T16:50:35.790
Yes it is necessary for the scaling of the picture for larger N. 7 significant figures on a 1000000 x 1000000 image corresponds to 0.1 pixels, but with intermediate calculations it could be worse than that. I just think
stroke-width:3.464102and similar is a bit excessive if the idea was to get 1 pixel accuracy. I will go ahead and include it like that, though, if that is the ruling. – Level River St – 2016-05-15T17:47:15.870