13
3
Introduction
The two most common trigonometric functions, sine and cosine (or sin and cos for short), can be extended to be matrix-valued functions. One way to compute the matrix-valued analogs is as follows:
Consider these two important trigonometric identities:
Using these identities, we can derive the following equations for sin and cos:
The matrix exponential exists for all square matrices and is given by:
where A0 is the identity matrix I with the same dimensions as A. Using the matrix exponential, these two trigonometric functions (and thus all the other trigonometric functions) can be evaluated as functions of matrices.
The Challenge
Given a square matrix A, output the values of sin(A) and cos(A).
Rules
- Input and output may be in any convenient, reasonable format (2D array, your language's matrix format, etc.).
- You may write a single program, two independent programs, a single function, or two functions. If you choose to write two functions, code may be shared between them (such as imports and helper functions).
- The input matrix's values will always be integers.
- Your solution may have accuracy issues as the result of floating-point imprecision. If your language had magical infinite-precision values, then your solution should work perfectly (ignoring the fact that it would require infinite time and/or memory). However, since those magical infinite-precision values don't exist, inaccuracies caused by limited precision are acceptable. This rule is in place to avoid complications resulting from requiring a specific amount of precision in the output.
- Builtins which compute trigonometric functions for matrix arguments (including hyperbolic trig functions) are not allowed. Other matrix builtins (such as multiplication, exponentiation, diagonalization, decomposition, and the matrix exponential) are allowed.
Test Cases
Format: A -> sin(A), cos(A)
[[0]] -> [[0]], [[1]]
[[0, 2], [3, 5]] -> [[-0.761177343863758, 0.160587281888277], [0.240880922832416, -0.359709139143065]], [[0.600283445979886, 0.119962280223493], [0.179943420335240, 0.900189146538619]]
[[1, 0, 1], [0, 0, 0], [0, 1, 0]] -> [[0.841470984807897, -0.158529015192103, 0.841470984807897], [0, 0, 0], [0, 1, 0]], [[0.540302305868140, -0.459697694131860, -0.459697694131860], [0, 1, 0], [0, 0, 1]]
[[1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]] -> [[0.841470984807897, 0, 0, 0, 0], [0, 0.841470984807897, 0, 0, 0], [0, 0, 0.841470984807897, 0, 0], [0, 0, 0, 0.841470984807897, 0], [0, 0, 0, 0, 0.841470984807897]], [[0.540302305868140, 0, 0, 0, 0], [0, 0.540302305868140, 0, 0, 0], [0, 0, 0.540302305868140, 0, 0], [0, 0, 0, 0.540302305868140, 0], [0, 0, 0, 0, 0.540302305868140]]
[[-3, 2, -6], [3, 0, 4], [4, -2, 7]] -> [[-0.374786510963954, 0.135652884035570, -1.35191037980742], [1.14843105375406, 0.773644542790111, 1.21625749577185], [1.21625749577185, -0.135652884035570, 2.19338136461532]], [[4.13614256031450, -1.91289828483056, 5.50873853927692], [-2.63939111203107, 1.49675144828342, -3.59584025444636], [-3.59584025444636, 1.91289828483056, -4.96843623340878]]
Further Reading
This excellent question over at Math.SE includes some alternate derivations of the matrix-valued analogs of trigonometric functions.

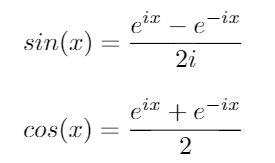
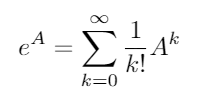
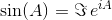
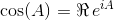

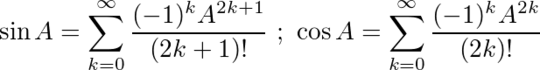
I got
sin([[1, 0, 1], [0, 0, 0], [0, 1, 0]]) = {{0.841, -0.158, 0.841}, {0, 0, 0}, {0, 1, 0}}with Mathematica, can you check? – kennytm – 2016-05-05T17:37:14.3871@kennytm That is what the test case shows. – Mego – 2016-05-05T17:38:01.250
So it is disallowed to sum some terms of the series, because adding a finite number of terms does not give an infinitely accurate value? – feersum – 2016-05-05T18:51:05.270
@feersum Correct. Unless it converges in a finite number of terms (which it doesn't), that's not a valid approach. – Mego – 2016-05-05T19:25:34.243
1@Mego Apparently all of the existing answers should be deleted then. – feersum – 2016-05-05T19:30:26.803
@feersum There are other ways to compute the matrix exponential other than just evaluating the series, such as diagonalization/Jordan decomposition. It's fair to assume that a builtin would use one of the more robust methods, rather than summing a finite number of terms of the sequence. – Mego – 2016-05-05T19:32:54.960
3@Mego It's completely unreasonable to think that all of the floating-point based builtins use an exact algorithm (or one that would be exact if floating-point operations were replaced with "real number" operations). – feersum – 2016-05-05T19:35:03.710
I'm not sure I'm interpreting this discussion correctly, but irrational numbers cannot be represented exactly as decimals or floating point numbers, unless you have both infinite memory to store the representation and infinite time to calculate its value. My answer keeps adding terms of the Taylor series until the result no longer changes. It gives an inaccurate result, but its accuracy increases as the precision of the floating point type increases. Is that allowed? – Dennis – 2016-05-05T19:41:25.307
@feersum I tried to make this as simple as possible when writing the challenge. Let me try stating it a different way: Use matrix exponential builtins if you want. Don't worry about inaccuracies due to limited precision with floating point values. Assume that, if your language had magical infinite-precision numeric values, the builtins would use them and everything would work like you expect. – Mego – 2016-05-05T19:46:36.237
@Dennis I'm going to allow that approach. What I specifically meant when I said that summing a finite number of terms was not valid was, if you sum some
Nterms of the series, whereNis constant, it's not valid. If you sum terms of the series until the delta hits 0, that's valid (becauseNwould be dependent on the precision of the numeric values, rather than a constant). Summing 5 terms and calling it good enough is not ok. Summing terms until they go below the machine/language floating point epsilon is ok. – Mego – 2016-05-05T19:50:03.003Summing until the delta becomes zero would fail if the language did have infinite precision values as the program would not halt. – feersum – 2016-05-05T19:51:41.747
1@feersum I've addressed that in my latest edit:
(ignoring the fact that it would require infinite time and/or memory)– Mego – 2016-05-05T19:52:38.377Hrm. The current conditions sound like they forbid the technique of using the recurrence
(cos(x) ,sin(x)) = (2 cos(x/2)^2 - 1, 2 sin(x/2) cos(x/2))until the argument is small enough that you can just usecos(x) = 1 - x^2/2andsin(x) = x. – None – 2016-05-05T23:11:22.647(1) I've fixed that. (2) I'm rather sure that they do. (3) The notion of well-ordering has no relation to this topic. There are plenty of norms one can put on matrices. (4) The same technique works for negative real numbers. – None – 2016-05-05T23:19:31.243