6
1
Gamma function is defined as
It is a well-known fact that for positive integers it coincides with a properly shifted factorial function: Γ(n) = (n - 1)!. However, a less famous fact is
Γ(1/2) = π1/2
Actually, the Gamma function can be evaluated for all half-integer arguments, and the result is a rational number multiplied by π1/2. The formulas, as mentioned in Wikipedia, are:
In this challenge, you should write code (program or function) that receives an integer n and returns the rational representation of Γ(1/2 + n) / π1/2, as a rational-number object, a pair of integers or a visual plain-text representation like 15/8.
The numerator and denominator don't need to be relatively prime. The code should support values of n at least in the range -10 ... 10 (I chose 10 because 20! < 264 and 19!! < 232).
Test cases (taken from Wikipedia):
Input | Output (visual) | Output (pair of numbers)
0 | 1 | 1, 1
1 | 1/2 | 1, 2
-1 | -2 | -2, 1
-2 | 4/3 | 4, 3
-3 | -8/15 | -8, 15
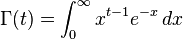
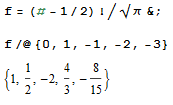
What kind of built-ins are allowed/forbidden? Gamma function? Pi function? – Dennis – 2016-05-03T22:21:32.677
All built-ins are allowed (it's the default, isn't it?): gamma-function, factorial, whatever. – anatolyg – 2016-05-03T22:23:39.287
Can I use the letter
rinstead of/? – Conor O'Brien – 2016-05-03T23:15:11.463Yes (just because I want to know how that would give you an advantage). – anatolyg – 2016-05-03T23:24:30.910
J uses
r(rational) as fraction separator. – Dennis – 2016-05-03T23:43:01.053This is a subset of http://codegolf.stackexchange.com/questions/63887/gamma-function-golf
– Mego – 2016-05-04T04:18:17.557@Mego Except that this requires exact rational output. – user202729 – 2018-03-04T10:28:07.247
@user202729 Hence why I just commented (nearly a year ago), rather than closing it as a dupe – Mego – 2018-03-04T15:42:15.410