Need help golfing Python 3 code to calculate volume & surface of spheroids in <150 bytes

Question

I want to write a function golf(C, A) that takes the height (C = 2*c) and the width (A = 2*a) of an oblate (left image) or prolate (right image) spheroid or a sphere as parameters and returns the volume V and the surface area S of the shape as tuple. The output must be rounded to two decimal places.

All input and output numbers are floating point decimals.
The input numbers (A and C) are guaranteed to be greater than 0 and lower than 100.

Here are some example calls of the function (golf(C, A)) in Python 3 and the expected outputs given as test cases:

golf(4, 2)  # expected output (8.38, 21.48)
golf(2, 2)  # expected output (4.19, 12.57)
golf(2, 4)  # expected output (16.76, 34.69)

The challenge requires my code to be smaller than 150 characters.

I could not manage to solve it myself yet, my best solution in Python 3 still takes 220 characters:

from math import * 
def golf(C,A):
 c,a,V=C/2,A/2,pi/6*A*A*C;F=c*c/a**2;E=sqrt(1-(F if a>c else 1/F));S=4*pi*a*a if a==c else 2*pi*a*a*(1+(((1-E**2)/E)*atanh(E)if a>c else(c/(a*E))*asin(E)))
 return round(V,2),round(S,2)

---

The necessary formulas are taken from Wikipedia: Spheroid, here's a summary:

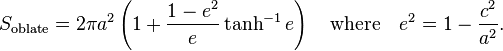
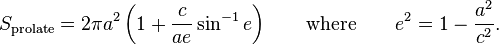
V_{all spheroids} = 4 π/3 a²c = π/6 A²C as A=2a and C=2c.

---

This challenge was originally from checkio.org and got refactored into a code-golf challenge for empireofcode.com.

Answer 1

122 bytes

from cmath import*
def golf(C,A):e=sqrt(1-A*A/C/C);return round(pi/6*A*A*C,2),round(pi*A*abs(A+(e and C*asin(e)/e-A)/2),2)

The sphere can be special-cased by returning surface area πA² if e = 0.

While there are two different formulae for oblate and prolate spheroids, they are mathematically equivalent. If the involved operations support complex numbers, each formula can be used for both cases.

Since asin(e)/e will return a complex number of the form x+0j for prolate spheroids, abs can be used to turn it into the float x.