Solve a Linear Equation

Question

^{This challenge but with a better spec.}

Spec

Your program will take a linear equation containing a single variable x and output the value of x.

Input / Parsing

• The input will only contain numbers, operators, parenthesis (()), x, and an = sign (this means no whitespace).
• Parenthesis will always be balanced.
• There will always be at least 1 x. An x may be preceded by a number.
• All equations will exactly have one result.

---

A number can be defined by following these steps. A number can be defined by the regex: -?(\d+(\.\d+)?|\.\d+).

---

If you don't speak regex: A digit is defined as 0-9

1. It may have a - at the beginning of it signifying negative
2. Then there may be some digits. If they aren't any digits there will be a decimal point
3. If a decimal point exists, at least one digit will follow it

The biggest a number / value will be is defined by your language's capabilities.

---

An operator is any of: +-*/, they will always appear between numbers, and or parenthesis

this means (5)(5) is not a valid input for the sake of simplicity.

---

Parenthesis will always contain a valid expression (a valid combination of numbers and/or operators) inside them. "Balanced" parenthesis is defined as every ( will have an associated closing )

Evaluation

• Order of operations should be followed and the precedences are (highest to lowest):
  • Parenthesis (most deeply nested first)
  • Multiplication & Division
  • Addition & Subtraction
• If two operators with the same precedence are occurred you should prefer going left -> right

Output

You should output the result in some way. If you don't output just number result, clarify in your answer how the output is outputted. Your output format should be consistent. Output may be a decimal, but it will always be rational, the precision is limited to your language's precision. Only if your language does not support floating point arithmetic, you do not need to support it.

Rules

• Built-ins trivializing this task are allowed but, you must clearly add [uses built-in] clearly to the header of the answer. This exempts your answer from winning
• A "Built-ins trivializing this task" is any of:
  • Something which takes in an equation and outputs the value for a/the variable
  • Something which will completely simplify an equation
  • Using eval or a related function to do a significant amount of the parsing. Use of eval and related functions are disallowed if they are used to (with minimal modification to the input) solve linear equations.
  • If you're in doubt, just ask in a comment.
• Built-ins which parse the equation are allowed

Examples

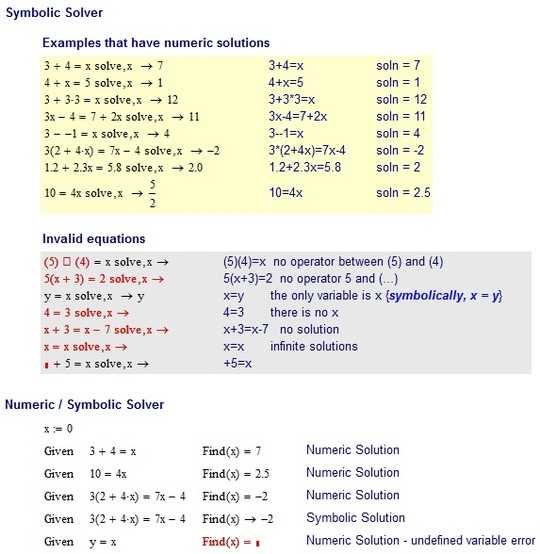
3+4=x
7

4+x=5
1

3+3*3=x
12

3x-4=7+2x
11

3--1=x
4

3*(2+4x)=7x-4
-2

1.2+2.3x=5.8
2

10=4x
2.5

INVALID Inputs:

(5)(4)=x  no operator between (5) and (4)
5(x+3)=2  no operator 5 and (...)
x=y       the only variable is x
4=3       there is no x
x+3=x-7   no solution
x=x       infinite solutions
+5=x      + is not an unary operator. -5=x would be valid though
1/(x-3)=5 Nonlinear
3/x       Nonlinear

Answer 1

JavaScript ES6, 246 bytes

Still some golfing to be done, but at least it's a solution!

C=a=>new Function("x","return "+a.replace(/(\d)x/g,"$1*x"));n=>{n=n.split("=");t=Math.abs,r=C(n[0]),c=C(n[1]),a=0,i=r(a)-c(a);a++;v=r(a)-c(a);o=t(i)<t(v)?-1:1;for(u=1/0;r(a)!==c(a);)a+=o,e=t(r(a)-c(a)),e>u&&(u=1/0,o/=10),u=Math.min(e,u);return a}

Name the function n=>{n=n.split("=")... to use it.

Hyper-ungolfed:

function solveLinear(equation){
    equation = equation.split("=");
    var abs = Math.abs;
    var LHS = convertToFunction(equation[0]), RHS = convertToFunction(equation[1]);
    var pivot = 0;
    var dir;
    var dir1 = LHS(pivot) - RHS(pivot);
    pivot++;
    var dir2 = LHS(pivot) - RHS(pivot);
    if(abs(dir1)<abs(dir2)) dir = -1;
    else dir = 1;
    var dif, minDif = Infinity;
    while(LHS(pivot) !== RHS(pivot)){
        pivot += dir;
        dif = abs(LHS(pivot) - RHS(pivot));
        if(dif > minDif){
            minDif = Infinity;
            dir /= 10;
        }
        minDif = Math.min(dif, minDif);
        console.log(pivot,dir,dif,minDif);
    }
    return {
        x: pivot,
        LHS: LHS,
        RHS: RHS
    };
}

This uses a pivot approach. (I'm not sure if this is what the algorithm is called, just a name I invented.) It first gathers which direction to search for from zero (i.e., which way the slopes of the two sides of the equations will intersect) and looks for the value. Once it finds a point of minimal difference, it goes to that point and decreases the search increment. This eventually yields as precise of a solution we need.

Answer 2

JavaScript (Node.js), 106 93 bytes

a=>eval(`f=x=>${a[R='replace'](/(\d)x/g,"$1*x")[R]("=","-(")[R](/-/g,"+-")})`)(0)/(f(0)-f(1))

Try it online!

-13 bytes thanks to @tsh

Ungolfed:

var h=a=>{
  a=a.replace(/(\d)x/g,"$1*x").replace("=","-(").replace("--","- -"); //get into an eval-able form
  var f=x=>eval(a+")");
  var df=(f(1)-f(0))/(1-0) //derivative or slope of the function
  var x=0;
  return x-(f(x)/df); //newton's method
}

Explaination:

This solution works by Newton's method for finding roots. The code subtracts the right hand side of the equation from the left hand side, such that when f(x)=0, x will equal the value we are solving for. Therefore, when we find the root of this new function, it will be our desired x value. Then it finds the derivative f'(x) by finding the slope between two points on the function. Then, the values are simply inserted into Newton's method which states for an approximation of the root x, x=x-(f(x)/f'(x)) (in the code, we use 0 as an initial x value). Since this finds the roots, it finds our x value. And since the equation is guaranteed to be linear, the approximation will be exact.

Answer 3

Mathcad, [uses built-in]

Mathcad has two built-in methods of solving such equations:

• Symbolic solver (uses the keyword solve)
• Solve Block (which works in both numeric and symbolic modes). A Solve Block starts with the keyword Given, followed a set of expressions defining the conditions of interest, and closed by one of the solving keywords, such as Find (which finds an exact solution) or MinErr (which minimizes the error between the target and any solution).

The symbolic solver is quite happy with y=x and returns the solution x = y.

For those unfamiliar with Mathcad, the image below is taken directly from the WYSIWYGish Mathcad 15 workbook. Changing any of the expressions where they are written will cause Mathcad to reevaluate its answer and update the display accordingly.

Answer 4

Axiom, 214 bytes [uses built-in]

q(t:EQ POLY FLOAT):Any==(a:=[variables(lhs t),variables(rhs t)];a.1~=[x]and a.1~=[]=>%i;a.2~=[x]and a.2~=[]=>%i;a.1=[]and a.2=[]=>%i;a.1=[x]and degree(lhs t,x)>1=>%i;a.2=[x]and degree(rhs t,x)>1=>%i;rhs solve(t).1)

For some error would return %i, for other type of errors the function is stopped from the system, something else as 1--2 seems out of language... test:

(72) -> q(x+3=9)
   (72)  6.0
                                  Type: Complex Fraction Polynomial Float
(73) -> q(3+4=x)
   (73)  7.0
                                  Type: Complex Fraction Polynomial Float
(74) -> q(4+x=5)
   (74)  1.0
                                  Type: Complex Fraction Polynomial Float
(75) -> q(3+3*3=x)
   (75)  12.0
                                  Type: Complex Fraction Polynomial Float
(76) -> q(3*x-4=7+2*x)
   (76)  11.0
                                  Type: Complex Fraction Polynomial Float
(77) -> q(3--1=x)
  Line   1: q(3--1=x)
           .AB
  Error  A: Missing mate.
  Error  B: syntax error at top level
  Error  B: Possibly missing a )
   3 error(s) parsing
(77) -> q(3*(2+4*x)=7*x-4)
   (77)  - 2.0
                                  Type: Complex Fraction Polynomial Float
(78) -> q(1.2+2.3*x=5.8)
   (78)  2.0
                                  Type: Complex Fraction Polynomial Float
(79) -> q(10=4*x)
   (79)  2.5
                                  Type: Complex Fraction Polynomial Float
(80) -> q((5)(4)=x)
   Cannot find a definition or applicable library operation named 5
      with argument type(s)
                           PositiveInteger

  Perhaps you should use "@" to indicate the required return type,
  or "$" to specify which version of the function you need.
(80) -> q(5(x+3)=2 )
   (80)  %i
                                                    Type: Complex Integer
(81) -> q(x=y)
   (81)  %i
                                                    Type: Complex Integer
(82) -> q(4=3)
   (82)  %i
                                                    Type: Complex Integer
(83) -> q(x+3=x-7)
   >> Error detected within library code:
   inconsistent equation
protected-symbol-warn called with (NIL)
(83) -> q(x=x)
   >> Error detected within library code:
   equation is always satisfied
protected-symbol-warn called with (NIL)