Addition on Elliptic Curves

Question

Addition on Elliptic Curves

_{Disclaimer: This does not do any justice on the rich topic of elliptic curves. It is simplified a lot. As elliptic curves recently got a lot of media attention in the context of encryption, I wanted to provide some small insight how "calculating" on an elliptic curve actually works.}

Introduction

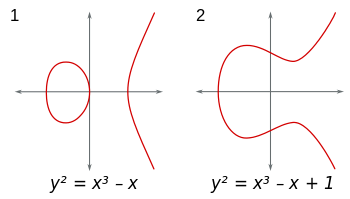
Elliptic curves are sets of points (x,y) in the plane of the form y^2 = x^3+Ax+B. (Additionally, 4A^3+27B^2 ≠ 0 to avoid nasty singularities.) You can consider these curves in any field. If you use the field of real numbers, the curves can be visualized and they look like this:

_Source

The special thing about these curves is that they have a built in arithmetic operation that is the analogue of addition. You can add and subtract points, and this operation is both associative and commutative (an abelian group).

How does addition work?

Note: addition of points on elliptic curves is not intuitive. This kind of addition is defined the way it is because it has certain nice properties. It's weird, but it works.

As elliptic curves form a group, there is an additive identity that is the equivalent of 0. That is, adding 0 to any point will not change the result. This additive identity is the "point" at infinity. All lines on the plane include this point at infinity, so adding it makes no difference.

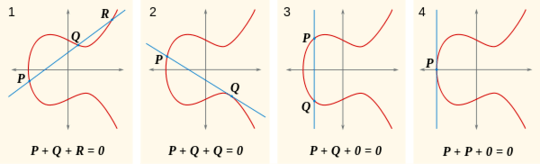
Let's say that any given line intersects the curve at three points, which may be 0, and that the sum of these three points is 0. Keeping that in mind, take a look at this image.

_Source

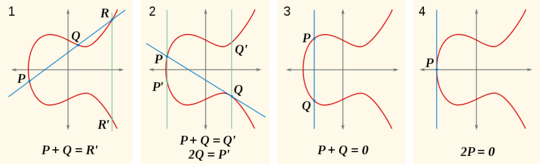
Now, the natural question is, what is P+Q? Well, if P+Q+R = 0, then P+Q = -R (alternatively written as R'). Where is -R? It is where R + (-R) = 0, which is on the other side of the x-axis from R so that the line through them is vertical, intersecting only R, -R, and 0. You can see this in the first part of this image:

_Source

Another thing you can see in these images is that the sum of a point with itself means the line is tangent to the curve.

How to find intersections of lines and elliptic curves

In the case of two distinct points

Generally there is exactly one line through two points P=(x0,y0), Q=(x1,y1). Assuming it is not vertical and the two points are distinct, we can write it as y = m*x+q. When we want to find the points of intersection with the elliptic curve we can just write

0 = x^3+Ax+B-y^2 = x^3+Ax+B-(m*x+q)^2

which is a third degree polynomial. These are generally not that easy to solve, but we already know two zeros of this polynomial: The two x-coordinates x0, x1 of the two points we want to add!

That way we factor out the linear factors (x-x0) and (x-x1) and are left with a third linear factor whose root is the x-coordinate of the point R. (-R too because of the symmetry. Note that if R = (x2,y2) then -R = (x2,-y2). The - is from the group; it is not a vectorial minus.)

In the case of adding one point P to itself

In this case we have to calculate the tangent of the curve at P=(x0,y0). We can directly write m and q in terms of A,B,x0,y0:

     3*x0^2 + A
m = ------------
        2*y0

     -x0^3 + A*x0 + 2*B
q = --------------------
          2*y0

We get the equation y = m*x+q and can proceed the same way as in the paragraph above.

A complete case tree

This is a complete list of how to handle all those cases:

Let P,Q be points on the elliptic curve (including the "infinity" point 0)

• If P = 0 or Q = 0, then P+Q = Q or P+Q = P, respectively
• Else P ≠ 0 and Q ≠ 0, so let P = (x0,y0) and Q = (x1,y1):
  • If P = -Q (that means x0 = x1 and y0 = -y1) then P+Q = 0
  • Else P ≠ -Q
    • If x0 = x1 then we have P=Q and we calculate the tangent (see section above) in order to get R. Then P+Q = P+P = 2P = -R
    • Else: We can construct a line of the form y = m*x+y through those two points (see section above) in order to calculate R. Then P+Q=-R

Finite fields

For this challenge we will only consider fields of size p where p is prime (and because of some details p ≠ 2, p ≠ 3). This has the advantage that you can simply calculate mod p. The arithmetic in other fields is much more complicated.

This in this example we set p = 5 and all equalities here are congruences mod 5.

2+4 ≡ 6 ≡ 1
2-4 ≡ -2 ≡ 3
2*4 ≡ 8 ≡ 3
2/4 ≡ 2*4 ≡ 3 because 4*4 ≡ 16 ≡ 1, therefore 1/4 ≡ 4

Challenge

Given the parameters A,B of an elliptic curve, a prime field characteristic p and two points P,Q on the elliptic curve, return their sum.

• You can assume that the parameters A,B actually describe an elliptic curve, that means that 4A^3+27B^2 ≠ 0.
• You can assume that P,Q are actually points on the elliptic curve or the 0-point.
• You can assume that p ≠ 2,3 is prime.

Test Cases

I made a (not very elegant) implementation in MATLAB/Octave, that you can use for your own test cases: ideone.com I hope it is correct. It did at least reproduce a few calculations I made by hand.

Note the trivial test cases that work for all curves we consider here:

Adding zero: P+0 = P Adding the inverse: (x,y) + (x,-y) = 0

---

For p = 7, A = 0, B = 5 the two points P = (3,2) and Q = (6,2) are on the elliptic curve. Then following holds:

2*Q = Q+Q = P
2*P = P+P = (5,2)
3*P = P+P+P = (5,2)+P = (6,5)
4*P = P+P+P+P = (5,2)+(5,2) = (6,5)+(5,2) = Q

All the poins on the elliptic curve are (3,2),(5,2),(6,2),(3,5),(5,5),(6,5),0

---

For p = 13, A = 3, B = 8 we get

(1,8)+(9,7) = (2,10)
(2,3)+(12,11) = (9,7)
2*(9,6) = (9,7)
3*(9,6) = 0

---

For p = 17, A = 2, B = 2 and P=(5,1) we get

2*P = (6,3)
3*P = (10,6)
4*P = (3,1)
5*P = (9,16)
6*P = (16,13)
7*P = (0,6)
8*P = (13,7)
9*P = (7,6)
10*P = (7,11)

---

If you are really ambitious, take

p = 1550031797834347859248576414813139942411
A = 1009296542191532464076260367525816293976
x0 = 1317953763239595888465524145589872695690
y0 = 434829348619031278460656303481105428081
x1 = 1247392211317907151303247721489640699240
y1 = 207534858442090452193999571026315995117

and try to find a natural number n such that n*(x0,y0) = (x1,y1). Further information here.

Appendix

First of all a big THANK YOU to @El'endiaStarman for reviewing and editing my draft!

Why elliptic curves?

Well it might appear like some kind of arbitrary equation, but it is not, it is quite general: Generally we consider those geometric "shapes" in the projective plane (that is where the "infinity" is coming from. There we consider all homogeneous polynomials of third degree. (Those of lower or higher degree would be too difficult or just trivial to examine.) After applying some restrictions in order to get the nice properties we want, and after dehomogenizing those polynomials (projecting into one of three affine planes) we end up with equations like y^2+a*x*y+b*y = x^3+c*x^2+d*x+e This is an elliptic curve in the long Weierstrass form. These are basically the same curves as we considered, but just somewhat skewed. With a linear coordinate transform, you can easily make a short Weierstras equation out of that. example, which still hold all the interesting properties.

Why did we exclude p=2,3?

This has to do with the fact that for the short Weierstrass form we need the restriction 4A^3+27B^2 ≠ 0 in order to avoid singularities (more on that below). In a field of characteristic 2 we have 4 = 0 and in a field of characteristic 3 we have 27 = 0, this makes it impossible to have curves in short weierstrass form for those kinds of fields.

What are singularities?

If the equation 4A^3+27B^2=0 holds, we have singularities like following: As you see at those points you cannot find a derivative and therefore no tangent, which "kills" the operation. You might look at the equations y^2 = x^3 or y^2 = x^3-3*x+2

Why are they called elliptic curves anyway?

The reason is that equations of this shape pop up in elliptic integrals, e.g. which are what you get when you want to caclulate the e.g. the arclength of an ellipse. A short slideshow about the origin of the name.

What do they have to do with cryptography?

There are ways to compute nP = P+P+...+P very efficiently. This can be used for example in the Diffie Hellman key exchange. The modular arithmetic can be replaced by the addition on torsion subgroups, these are just the points on the curve that have finite order. (That means that mP = 0 for some m, which is basically just calculating mod m ).

Answer 1

Pyth, 105 100 bytes

A,@Q3eQ?qGZH?qHZG?&=YqhHhGqeG%_eHhQZ_m%dhQ,-*J?Y*+*3^hG2@Q1^*2eG-hQ2*-eGeH^-hGhH-hQ2-hGK--^J2hGhHeGK

Input is expected as (p, A, P, Q), where P and Q are the two points of the form (x, y) or, if they are the special 0 point, just as 0. You can try it out online here. The last two examples show how the special 0 works.

In order to save a few bytes, I only use mod p on the final answer. This means that it does things like x0^p a few times without doing modular exponentiation, so it might be very slow.

It works by following roughly the same logic as this Python function:

def add_ellip(p, A, P, Q): # points are in format (x, y)
    z = 0 # representing special 0 point

    if (P == z):
        return Q
    if (Q == z):
        return P

    if P[0] == Q[0]:
        if (P == (Q[0], -Q[1] % p)):
            return z
        else:
            m = ((3*pow(P[0], 2, p) + A)*pow(2*P[1], p-2, p)) % p
    else:
        m = (P[1] - Q[1])*pow(P[0] - Q[0], p-2, p) % p

    x = (pow(m, 2, p) - P[0] - Q[0]) % p
    y = (m*(P[0] - x) - P[1]) % p
    return (x, y)

This is heavily reliant on the fact that the modular multiplicative inverse of x is equal to x^(p-2) mod p if p is prime. Thus we are able to compute m, the slope of the line, by finding the modular multiplicative inverse of the denominator and multiplying it by numerator. Pretty handy. The Python function should calculate larger problems a little more efficiently because of the use of pow.

I also used the shortcuts shown on the Wikipedia page on this subject. It's quite interesting I only end up using A once, and B not at all.

Also just for fun:

def pow2floor(x):
    p = 1
    x >>= 1
    while (x > 0):
        x >>= 1
        p <<= 1
    return p

def multi_nP(p, A, n, P):
    d = {}

    def rec_helper(n, P):
        if (n == 0):
            return (0, 0)
        elif (n == 1):
            return P
        elif (n in d):
            return d[n]
        else:
            p2f = pow2floor(n)
            remainder = n - p2f

            lower_half = rec_helper(p2f//2, P)
            d[p2f//2] = lower_half
            nP = add_ellip(p, A, lower_half, lower_half)

            if (remainder):
                nP = add_ellip(p, A, nP, rec_helper(remainder, P))

            d[n] = nP
            return nP

    return rec_helper(n, P)

The multi_nP function computes n*P for a given integer n and point P. It uses a recursive strategy by splitting n into two parts p2f and remainder such that p2f + remainder = n and that p2f = 2^k. Then we call the function again on those parts, adding the result with add_ellip. I also used basic dynamic programming approach by saving already computed values in the dict d.

The next function would theoretically solve the bonus question using the same strategy:

def find_nPQ(p, A, P, Q): # P is input point, Q is what we're looking for
    d = {}
    found_Q = False

    def rec_helper(n, P):
        if (n == 0):
            return (0, 0)
        elif (n == 1):
            return P
        elif (n in d):
            return d[n]
        else:
            p2f = pow2floor(n)
            remainder = n - p2f

            lower_half = rec_helper(p2f//2, P)
            d[p2f//2] = lower_half

            nP = add_ellip(p, A, lower_half, lower_half)

            if (remainder):
                nP = add_ellip(p, A, nP, rec_helper(remainder, P))

            d[n] = nP
            return nP


    for x in range(p):
        xP = rec_helper(x, P)
        if (xP == Q):
            return x

Unfortunately, it runs nowhere near quickly enough to compute it. I'm guessing there might be much more efficient ways to do this, especially if we don't have to iterate through every possibly value for n.

Answer 2

Python 3, 193 191 bytes

A solution based on Rhyzomatic's Pyth answer and their Python logic. In particular. I liked how they found the third root of a monic cubic polynomial x^3 + bx^2 + cx + d when you have two roots x_1 and x_2 by noting that b == x_1 + x_2 + x_3 and subtracting accordingly. I plan to add an explanation, golf this, and perhaps transpile it into Ruby, if Ruby turns out to be shorter.

def e(p,A,B,P,Q):
 if P==0:return Q
 if Q==0:return P
 f,g=P;j,k=Q
 if f==j:
  if g==-k%p:return 0
  m=(3*f*f+A)*pow(2*j,p-2)
 else:m=(g-k)*pow(f-j,p-2)
 x=m*m-f-j;y=m*(f-x)-g;return(x%p,y%p)

Ungolfing:

def elliptic_curve_addition(p, A, B, P, Q):
    if P == 0:
        return Q
    if Q == 0:
        return P
    f,q = P
    j,k = Q
    if f==j:
        if g == (-k) % p:
            return 0
        m = (3 * f**2 + A) * pow(2*j, p-2)
    else:
        m = (g-k) * pow(f-j, p-2)
    x = m**2 - f - j
    y = m * (f-x) - g
    return (x%p, y%p)