11
2
Introduction
I found this question that was closed because it was unclear, yet it was a nice idea. I'll do my best to make this into a clear challenge.
The Riemann Zeta function is a special function that is defined as the analytical continuation of
to the complex plane. There are many equivalent formulas for it which makes it interesting for code golf.
Challenge
Write a program that takes 2 floats as input (the real and imaginary part of a complex number) and evaluates the Riemann Zeta function at that point.
Rules
- Input and output via console OR function input and return value
- Built in complex numbers are not allowed, use floats (number, double, ...)
- No mathematical functions except
+ - * / pow logand real valued trig functions (if you want to integrate, use the gamma function, ... you must include this functions definition in the code) - Input: 2 floats
- Output: 2 floats
- Your code must contain value that gives theoretically arbitrary precision when made arbitrary large/small
- The behaviour at input 1 is not important (this is the only pole of this function)
Shortest code in bytes wins!
Example Input and Output
Input:
2, 0
Output:
1.6449340668482266, 0
Input:
1, 1
Output:
0.5821580597520037, -0.9268485643308071
Input:
-1, 0
Output:
-0.08333333333333559, 0
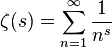
1What's the required output precision? I'm not sure I understand Your code must contain value that gives theoretically arbitrary precision when made arbitrary large/small. Do you mean like a loop maximum value than when increased without bound gives increased precision? Can that value be hard-coded? – Luis Mendo – 2016-03-10T16:32:49.383
@DonMuesli This means the precision depends on a parameter, say N, which you may give any value you like, but for any given precision, you can make N small or large enough to achieve that precision. The word theoretically is there because you must not worry about the limited precision of the machine or language. – Jens Renders – 2016-03-10T16:35:17.937
To further clarify N: is it sufficient that for any bound
epsand inputxthere exists anNwhich calculateszeta(x)to withineps; or must there exist anNwhich depends only onepsand guarantees that for anyx(or perhaps for anyxmore than a given function ofepsfrom the pole) it achieves the bound; or mayNdepend onx, but answers should explain how to calculateNgivenxandeps? (My analytical number theory isn't up to much, but I suspect that options 2 and 3 are going to be beyond all but one or two regular posters). – Peter Taylor – 2016-03-10T18:59:48.067@PeterTaylor N large enough: For any
xand for anyepsthere must exist aPsuch that for allN>Pthe output is closer thanepsto the exact value. Is this clear? Do I need to clarify it for the case with N small enough? – Jens Renders – 2016-03-10T19:27:36.633No, that's clear enough. – Peter Taylor – 2016-03-10T20:40:08.183