25
1
Given a vector of n values (x1,x2,x3,...,xn) return the determinant of the corresponding Vandermonde matrix.
This determinant can be written as:
Details
Your program/function has to accept a list of floating point numbers in any convenient format that allows for a variable length, and output the specified determinant.
You can assume that the input as well as the output is within the range of the values your language supports. If you language does not support floating point numbers, you may assume integers.
Some test cases
Note that whenever there are two equal entries, the determinant will be 0 as there are two equal rows in the corresponding Vandermonde matrix. Thanks to @randomra for pointing out this missing testcase.
[1,2,2,3] 0
[-13513] 1
[1,2] 1
[2,1] -1
[1,2,3] 2
[3,2,1] -2
[1,2,3,4] 12
[1,2,3,4,5] 288
[1,2,4] 6
[1,2,4,8] 1008
[1,2,4,8,16] 20321280
[0, .1, .2,...,1] 6.6586e-028
[1, .5, .25, .125] 0.00384521
[.25, .5, 1, 2, 4] 19.3798828
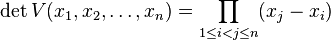
Can we assume the input is at least of length 2? – PurkkaKoodari – 2016-03-04T21:00:35.080
@Pietu1998 No, see the first test case. – Alex A. – 2016-03-04T21:02:57.197
3Important test case:
[1,2,2,3] => 0: two equal elements in the array, to test if the code checks self-difference (xi-xi) just by comparing to0. – randomra – 2016-03-05T11:10:36.163@randomra Thank you, I totally forgot to include one of those. Whenever two entries are equal, the determinant will be 0 as there are two times the same row. – flawr – 2016-03-07T20:39:55.700
1@flawr The expected output was clear from your specs. I suggested the test case so answers not prepared for equal numbers could find their mistakes more easily. – randomra – 2016-03-07T21:19:39.790