19 NANDs
There is no simpler circuit than this.
There is code for testing it below the picture.
As for understanding it, that's difficult.
There are a couple of IF gates there, and the inputs are kinda grouped into a triangle with the free corner lines added for analysis one by one, but not in a simple way. If anyone manages to understand it, I will be impressed.
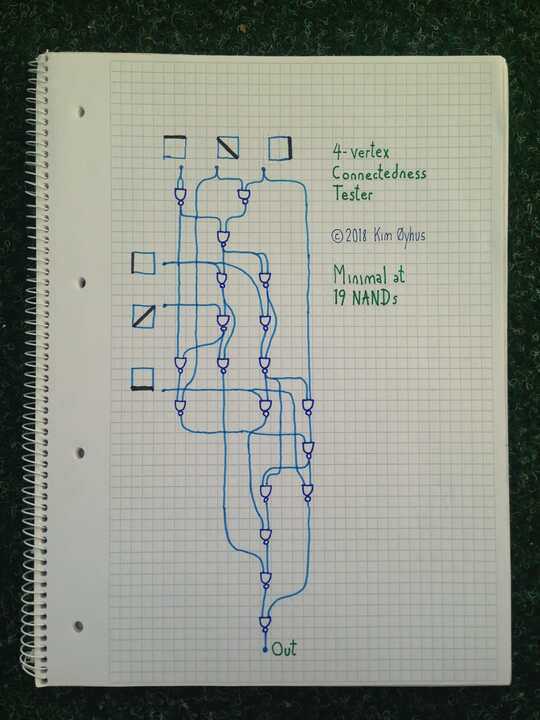
Verilog code with testing:
// 4-vertex Connectedness Tester
// Minimal at 19 NANDs
//
// By Kim Øyhus 2018 (c) into (CC BY-SA 3.0)
// This work is licensed under the Creative Commons Attribution 3.0
// Unported License. To view a copy of this license, visit
// https://creativecommons.org/licenses/by-sa/3.0/
//
// This is my entry to win this Programming Puzzle & Code Golf
// at Stack Exchange:
// https://codegolf.stackexchange.com/questions/69912/build-a-4-vertex-connectedness-tester-using-nand-gates/
//
// I am sure there are no simpler solutions to this problem.
// It has a logical depth of 11, which is deeper than
// circuits using a few more NANDs.
module counting6 ( in_000, in_001, in_002, in_003, in_004, in_005, in_006, out000 );
input in_000, in_001, in_002, in_003, in_004, in_005, in_006;
output out000;
wire wir000, wir001, wir002, wir003, wir004, wir005, wir006, wir007, wir008, wir009, wir010, wir011, wir012, wir013, wir014, wir015, wir016, wir017;
nand gate000 ( wir000, in_000, in_000 );
nand gate001 ( wir001, in_001, in_003 );
nand gate002 ( wir002, wir001, wir000 );
nand gate003 ( wir003, in_002, wir002 );
nand gate004 ( wir004, wir002, wir002 );
nand gate005 ( wir005, wir004, in_002 );
nand gate006 ( wir006, wir005, wir004 );
nand gate007 ( wir007, in_005, wir006 );
nand gate008 ( wir008, in_003, wir006 );
nand gate009 ( wir009, in_004, wir003 );
nand gate010 ( wir010, wir003, wir009 );
nand gate011 ( wir011, wir009, wir000 );
nand gate012 ( wir012, wir011, in_001 );
nand gate013 ( wir013, wir008, wir012 );
nand gate014 ( wir014, wir013, in_005 );
nand gate015 ( wir015, wir006, wir013 );
nand gate016 ( wir016, wir015, wir007 );
nand gate017 ( wir017, wir016, wir010 );
nand gate018 ( out000, wir014, wir017 );
endmodule
module connecting6_test;
reg [5:0] X;
wire a;
counting6 U1 (
.in_000 (X[0]),
.in_001 (X[1]),
.in_002 (X[2]),
.in_003 (X[3]),
.in_004 (X[4]),
.in_005 (X[5]),
.in_006 (X[6]),
.out000 (a )
);
initial begin
X = 0;
end
always
#10 X = X+1;
initial begin
$display("\t\t \t_");
$display("\t\ttime,\t \\db/_,\tconnected");
$monitor("%d,\t%b,\t%d",$time, X, a );
end
initial
#630 $finish;
endmodule
// iverilog -o hello hello.v
// vvp hello
Kim Øyhus

Could you specify the input format further? – LegionMammal978 – 2016-01-23T02:23:13.710
iej is True or False according to whether there is or isn't an edge from vertex i to vertex j.
– None – 2016-01-23T02:26:21.773Can input be taken as
0and1? How about output? – TheCoffeeCup – 2016-01-23T02:37:10.1603@TheCoffeeCup This is a logic circuit design problem, not [tag:code-golf]. – lirtosiast – 2016-01-23T02:39:38.637
@ThomasKwa Whoops, did not notice. – TheCoffeeCup – 2016-01-23T02:41:15.510
Why such a small input space? – Michael Klein – 2016-01-23T04:01:56.550
@MichaelKlein : It seemed like enough optimization would already be possible with only 4 vertices. – None – 2016-01-23T04:48:02.387
Can the output of a gate be used for multiple other gates? Equivalently, can we save the result of a partial computation to a variable? Also, do we have access to the constants 0 and 1? – xnor – 2016-01-23T08:37:44.870
@xnor : Yes. Since a "gate's 2 inputs can be the same input bit or other gate", [a gate that has exactly one constant-1 input can be replaced with a gate that doesn't have any constant-1 inputs] and otherwise, a gate with one or two constant inputs can be removed. Since there are connected 4-vertes graphs and disconnected 4-vertex graphs, the output node can't be a constant, so by induction, "the constants 0 and 1" can't help. – None – 2016-01-23T09:21:45.057
Can a gate have more than two inputs? – LegionMammal978 – 2016-01-23T12:19:53.590
@LegionMammal978 : No. – None – 2016-01-23T12:43:51.410