13
A polynomial with coefficients in some field F is called irreducible over F if it cannot be decomposed into the product of lower degree polynomials with coefficients in F.
Consider polynomials over the Galois field GF(5). This field contains 5 elements, namely the numbers 0, 1, 2, 3, and 4.
Task
Given a positive integer n, compute the number of irreducible polynomials of degree n over GF(5). These are simply the polynomials with coefficients in 0-4 which cannot be factored into other polynomials with coefficients in 0-4.
Input
Input will be a single integer and can come from any standard source (e.g. STDIN or function arguments). You must support input up to the largest integer such that the output does not overflow.
Output
Print or return the number of polynomials that are irreducible over GF(5). Note that these numbers get large rather quickly.
Examples
In : Out
1 : 5
2 : 10
3 : 40
4 : 150
5 : 624
6 : 2580
7 : 11160
8 : 48750
9 : 217000
10 : 976248
11 : 4438920
Note that these numbers form the sequence A001692 in OEIS.
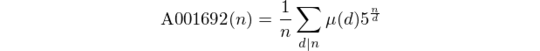
PARI/GP 46 bytes on A001692 ;) Is there a time limit? – ბიმო – 2016-01-18T04:39:42.797
@Bruce_Forte Nope. – Alex A. – 2016-01-18T04:42:35.213